D
分析:據(jù)兩直線(xiàn)相交斜率不等,求出a,b滿(mǎn)足的條件,據(jù)古典概型概率公式求出P
1,P
2,據(jù)復(fù)數(shù)的集合意義求出點(diǎn)P坐標(biāo),判斷出與直線(xiàn)的關(guān)系.
解答:易知當(dāng)且僅當(dāng)
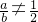
時(shí)兩條直線(xiàn)只有一個(gè)交點(diǎn),
而
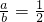
的情況有三種:a=1,b=2(此時(shí)兩直線(xiàn)重合);a=2,b=4(此時(shí)兩直線(xiàn)平行);a=3,b=6(此時(shí)兩直線(xiàn)平行).
而投擲兩次的所有情況有6×6=36種,
所以?xún)蓷l直線(xiàn)相交的概率

;
兩條直線(xiàn)平行的概率為P
1=

,
P
1+P
2i所對(duì)應(yīng)的點(diǎn)為P
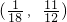
,
易判斷P
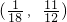
在l
2:x+2y=2的左下方,
故選項(xiàng)為D.
點(diǎn)評(píng):本題融合了直線(xiàn)、線(xiàn)性規(guī)劃、概率及復(fù)數(shù)等有關(guān)知識(shí),在處理方法上可采用枚舉法處理,注意不等忽視了直線(xiàn)重合這種情況,否則會(huì)選C.

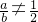 時(shí)兩條直線(xiàn)只有一個(gè)交點(diǎn),
時(shí)兩條直線(xiàn)只有一個(gè)交點(diǎn),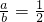 的情況有三種:a=1,b=2(此時(shí)兩直線(xiàn)重合);a=2,b=4(此時(shí)兩直線(xiàn)平行);a=3,b=6(此時(shí)兩直線(xiàn)平行).
的情況有三種:a=1,b=2(此時(shí)兩直線(xiàn)重合);a=2,b=4(此時(shí)兩直線(xiàn)平行);a=3,b=6(此時(shí)兩直線(xiàn)平行). ;
; ,
,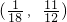 ,
,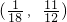 在l2:x+2y=2的左下方,
在l2:x+2y=2的左下方,

