
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)若直線![]() 與圓
與圓![]() 相交于
相交于![]() ,
,![]() 兩點,求弦長
兩點,求弦長![]() ,若點
,若點![]() ,求
,求![]() 的值;
的值;
(2)以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,圓
軸的非負半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() ,圓
,圓![]() 和圓
和圓![]() 的交點為
的交點為![]() ,
,![]() ,求弦
,求弦![]() 所在直線的直角坐標方程.
所在直線的直角坐標方程.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分別是棱
分別是棱![]() 、
、![]() 上的動點,且
上的動點,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
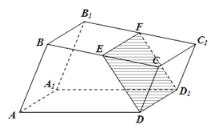
(1)證明:無論點![]() 怎樣運動,四邊形
怎樣運動,四邊形![]() 都為矩形;
都為矩形;
(2)當![]() 時,求幾何體
時,求幾何體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學理科成績優異,今年參加了數學,物理,化學,生物4門學科競賽.已知該同學數學獲一等獎的概率為![]() ,物理,化學,生物獲一等獎的概率都是
,物理,化學,生物獲一等獎的概率都是![]() ,且四門學科是否獲一等獎相互獨立.
,且四門學科是否獲一等獎相互獨立.
(1)求該同學至多有一門學科獲得一等獎的概率;
(2)用隨機變量![]() 表示該同學獲得一等獎的總數,求
表示該同學獲得一等獎的總數,求![]() 的概率分布和數學期望
的概率分布和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視臺問政直播節目首場內容是“讓交通更順暢”.A、B、C、D四個管理部門的負責人接受問政,分別負責問政A、B、C、D四個管理部門的現場市民代表(每一名代表只參加一個部門的問政)人數的條形圖如下.為了了解市民對武漢市實施“讓交通更順暢”幾個月來的評價,對每位現場市民都進行了問卷調查,然后用分層抽樣的方法從調查問卷中抽取20份進行統計,統計結果如下面表格所示:
滿意 | 一般 | 不滿意 | |
A部門 | 50% | 25% | 25% |
B部門 | 80% | 0 | 20% |
C部門 | 50% | 50% | 0 |
D部門 | 40% | 20% | 40% |

(1)若市民甲選擇的是A部門,求甲的調查問卷被選中的概率;
(2)若想從調查問卷被選中且填寫不滿意的市民中再選出2人進行電視訪談,求這兩人中至少有一人選擇的是D部門的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() (
(![]() ),圓
),圓![]() (
(![]() ),若圓
),若圓![]() 的一條切線
的一條切線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點.
兩點.
(1)當![]() ,
, ![]() 時,若點
時,若點![]() 都在坐標軸的正半軸上,求橢圓
都在坐標軸的正半軸上,求橢圓![]() 的方程;
的方程;
(2)若以![]() 為直徑的圓經過坐標原點
為直徑的圓經過坐標原點![]() ,探究
,探究![]() 是否滿足
是否滿足![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點M在橢圓![]()
![]() 上,以M為圓心的圓與x軸相切于橢圓的右焦點F.
上,以M為圓心的圓與x軸相切于橢圓的右焦點F.
(Ⅰ)若圓M與y軸相切,求橢圓的離心率;
(Ⅱ)若圓M與y軸相交于A,B兩點,且![]() 是邊長為2的正三角形,求橢圓的方程.
是邊長為2的正三角形,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 滿足:
滿足:![]() ,
,![]() .
.![]() 的前n項和為
的前n項和為![]() .
.
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)若![]() ,
,![]() (
(![]() ),求數列
),求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() =
=![]()
【解析】
試題分析:(Ⅰ)設出首項a1和公差d ,利用等差數列通項公式,就可求出![]() ,再利用等差數列前項求和公式就可求出
,再利用等差數列前項求和公式就可求出![]() ;(Ⅱ)由(Ⅰ)知
;(Ⅱ)由(Ⅰ)知![]() ,再利用
,再利用![]() ,
,![]() (
(![]() ),就可求出
),就可求出![]() ,再利用錯位相減法就可求出
,再利用錯位相減法就可求出![]() .
.
試題解析:(Ⅰ)設等差數列{an}的首項為a1,公差為d
∵ ![]() ,
,![]() ∴
∴ ![]() 解得
解得 ![]()
∴ ![]()
![]() ,
,
(Ⅱ)∵ ![]() ,
,![]() ∴
∴ ![]()
∵![]() ∴
∴ ![]()
∴ ![]()
![]()
![]()
= ![]() (1-
(1- ![]() +
+ ![]() -
- ![]() +…+
+…+![]() -
-![]() )
)
=![]() (1-
(1-![]() ) =
) =![]()
所以數列![]() 的前
的前![]() 項和
項和![]() =
=![]() .
.
考點:1.等差數列的通項公式; 2. 等差數列的前n項和公式; 3.裂項法求數列的前n項和公式
【題型】解答題
【結束】
18
【題目】在如圖所示的幾何體中,四邊形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
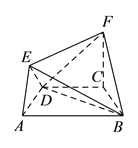
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在線段
)在線段![]() (含端點)上,是否存在一點
(含端點)上,是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com