【題目】給出下列函數：
①y=x+ 
；
②y=lgx+logx10（x＞0，x≠1）；
③y=sinx+ 
（0＜x≤ 
）；
④y= 
；
⑤y= 
（x+ 
）（x＞2）．
其中最小值為2的函數序號是 ．
【答案】③⑤
【解析】解：①y=x+ 
，當x＞0時，y有最小值2；x＜0時，有最大值﹣2；②y=lgx+logx10（x＞0，x≠1），x＞1時，有最小值2；0＜x＜1時，有最大值﹣2；
③y=sinx+ 
（0＜x≤ 
），t=sinx（0＜t≤1），y=t+ 
≥2 
=2，x= 最小值取得2，成立；
④y= 
= 
+ 
，t= （t≥ 
），y=t+ 遞增，t= 時，取得最小值 
；
⑤y= 
（x+ 
）（x＞2）= （x﹣2+ +2）≥ （2 
+2）=2，x=3時，取得最小值2．
所以答案是：③⑤．
【考點精析】通過靈活運用函數的最值及其幾何意義，掌握利用二次函數的性質（配方法）求函數的最大（小）值；利用圖象求函數的最大（小）值；利用函數單調性的判斷函數的最大（小）值即可以解答此題．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，△ABC中，已知頂點A（3，﹣1），∠B的內角平分線方程是x﹣4y+10=0過點C的中線方程為6x+10y﹣59=0．求頂點B的坐標和直線BC的方程．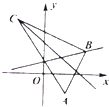 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}滿足an+1+an=4n﹣3（n∈N*）
（Ⅰ）若{an}是等差數列，求其通項公式；
（Ⅱ）若{an}滿足a1=2，Sn為{an}的前n項和，求S2n+1 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓
： 
，其左右焦點為
及
，過點
的直線交橢圓
于
， 
兩點，線段
的中點為
， 
的中垂線與
軸和
軸分別交于
， 
兩點，且
、
、
構成等差數列．
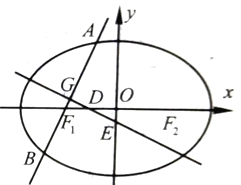
（1）求橢圓
的方程；
（2）記
的面積為
， 
（
為原點）的面積為
．試問：是否存在直線
，使得
？說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的一條對稱軸為
，且最高點的縱坐標是
．
（1）求
的最小值及此時函數
的最小正周期、初相；
（2）在（1）的情況下，設
，求函數
在
上的最大值和最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合M={1，2，3，4，5，6，7，8，9，10，11，12}，以下命題正確的序號是 ．
①如果函數f（x）=x（x﹣a1）（x﹣a2）…（x﹣a7），其中ai∈M（i=1，2，3，…，7），那么f′（0）的最大值為127 ．
②數列{an}滿足首項a1=2，ak+12﹣ak2=2，k∈N* ， 當n∈M且n最大時，數列{an}有2048個．
③數列{an}（n=1，2，3，…，8）滿足a1=5，a8=7，|ak+1﹣ak|=2，k∈N* ， 如果數列{an}中的每一項都是集合M的元素，則符合這些條件的不同數列{an}一共有33個．
④已知直線amx+any+ak=0，其中am ， an ， ak∈M，而且am＜an＜ak ， 則一共可以得到不同的直線196條．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知矩形
和菱形
所在平面互相垂直，如圖，其中
， 
， 
，點
為線段
的中點．
（Ⅰ）試問在線段
上是否存在點
，使得直線
平面
？若存在，請證明
平面
，并求出
的值，若不存在，請說明理由；
（Ⅱ）求二面角
的正弦值．
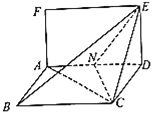
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
