
【題目】閱讀下列材料:
北京市正圍繞著“政治中心、文化中心、國際交往中心、科技創新中心”的定位,深入實施“人文北京、科技北京、綠色北京”的發展戰略.“十二五”期間,北京市文化創意產業展現了良好的發展基礎和巨大的發展潛力,已經成為首都經濟增長的支柱產業.
2011年,北京市文化創意產業實現增加值1938.6億元,占地區生產總值的12.2%.2012年,北京市文化創意產業繼續呈現平穩發展態勢,實現產業增加值2189.2億元,占地區生產總值的12.3%,是第三產業中僅次于金融業、批發和零售業的第三大支柱產業.2013年,北京市文化產業實現增加值2406.7億元,比上年增長9.1%,文化創意產業作為北京市支柱產業已經排到了第二位.2014年,北京市文化創意產業實現增加值2749.3億元,占地區生產總值的13.1%,創歷史新高,2015年,北京市文化創意產業發展總體平穩,實現產業增加值3072.3億元,占地區生產總值的13.4%.
根據以上材料解答下列問題:
(1)用折線圖將2011﹣2015年北京市文化創意產業實現增加值表示出來,并在圖中標明相應數據;
(2)根據繪制的折線圖中提供的信息,預估2016年北京市文化創意產業實現增加值約億元,你的預估理由 .
【答案】
(1)
解:(1)2011﹣2015年北京市文化創意產業實現增加值如圖所示,
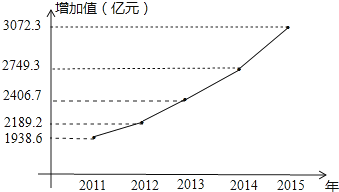
(2)3471.7;用近3年的平均增長率估計2016年的增長率
【解析】(2)解:設2013到2015的平均增長率為x,
則2406.7(1+x)2=3072.3,
解得x≈13%,
用近3年的平均增長率估計2016年的增長率,
∴2016年的增長率為3072.3×(1+13%)≈3471.7億元.
故答案分別為3471.7,用近3年的平均增長率估計2016年的增長率.
本題考查折線圖、樣本估計總體的思想,解題的關鍵是用近3年的平均增長率估計2016年的增長率,屬于中考常考題型.(1)畫出2011﹣2015的北京市文化創意產業實現增加值折線圖即可.(2)設2013到2015的平均增長率為x,列出方程求出x,用近3年的平均增長率估計2016年的增長率即可解決問題.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源: 題型:
【題目】如圖是將一正方體貨物沿坡面AB裝進汽車貨廂的平面示意圖.已知長方體貨廂的高度BC為 ![]() 米,tanA=
米,tanA= ![]() ,現把圖中的貨物繼續往前平移,當貨物頂點D與C重合時,仍可把貨物放平裝進貨廂,求BD的長.(結果保留根號)
,現把圖中的貨物繼續往前平移,當貨物頂點D與C重合時,仍可把貨物放平裝進貨廂,求BD的長.(結果保留根號)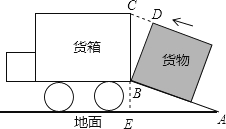
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線y=﹣ ![]() +bx+c與y軸交于點C,與x軸的兩個交點分別為A(﹣4,0),B(1,0).
+bx+c與y軸交于點C,與x軸的兩個交點分別為A(﹣4,0),B(1,0).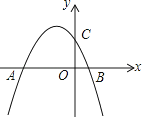
(1)求拋物線的解析式;
(2)已知點P在拋物線上,連接PC,PB,若△PBC是以BC為直角邊的直角三角形,求點P的坐標;
(3)已知點E在x軸上,點F在拋物線上,是否存在以A,C,E,F為頂點的四邊形是平行四邊形?若存在,請直接寫出點E的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2-2x+4y-4=0,
(1)求圓C關于直線![]() 對稱的圓的方程;
對稱的圓的方程;
(2)問是否存在斜率為1的直線l,使l被圓C截得弦AB,且以AB為直徑的圓經過點![]() ?若存在,求出直線l的方程;若不存在,說明理由.
?若存在,求出直線l的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某養殖場需定期購買飼料,已知該場每天需要飼料200千克,每千克飼料的價格為1.8元,飼料的保管費與其他費用平均每千克每天0.03元,購買飼料每次支付運費300元.
(1)求該場多少天購買一次飼料才能使平均每天支付的總費用最少;
(2)若提供飼料的公司規定,當一次購買飼料不少于5噸時,其價格可享受八五折優惠(即原價為85%).問:該場是否應考慮利用此優惠條件?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知y是x的函數,自變量x的取值范圍x>0,下表是y與x的幾組對應值:
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小騰根據學習函數的經驗,利用上述表格所反映出的y與x之間的變化規律,對該函數的圖象與性質進行了探究.
下面是小騰的探究過程,請補充完整:
(1)如圖,在平面直角坐標系xOy中,描出了以上表格中各對對應值為坐標的點,根據描出的點,畫出該函數的圖象;
(2)根據畫出的函數圖象,寫出:
①x=4對應的函數值y約為
②該函數的一條性質:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 的坐標為
的坐標為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,動點
,動點![]() 在圓
在圓![]() 上運動,點
上運動,點![]() 為
為![]() 延長線上一點,且
延長線上一點,且![]() .
.
(1)求點![]() 的軌跡方程.
的軌跡方程.
(2)過點![]() 作圓
作圓![]() 的兩條切線
的兩條切線![]() ,
, ![]() ,分別與圓
,分別與圓![]() 相切于點
相切于點![]() ,
, ![]() ,求直線
,求直線![]() 的方程,并判斷直線
的方程,并判斷直線![]() 與點
與點![]() 所在曲線的位置關系.
所在曲線的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)選修4—4:坐標系與參數方程
在直角坐標系xOy中,圓C的參數方程![]() 為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(1)求圓C的極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() 與圓C的交點為O、P,與直線
與圓C的交點為O、P,與直線![]() 的交點為Q,求線段PQ的長.
的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2016高考北京文數】某市居民用水擬實行階梯水價,每人月用水量中不超過w立方米的部分按4元/立方米收費,超出w立方米的部分按10元/立方米收費.從該市隨機調查了10 000位居民,獲得了他們某月的用水量數據,整理得到如下頻率分布直方圖:

(I)如果w為整數,那么根據此次調查,為使80%以上居民在該月的用水價格為4元/立方米,w至少定為多少?
(II)假設同組中的每個數據用該組區間的右端點值代替,當w=3時,估計該市居民該月的人均水費.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com