
【題目】已知雙曲線![]() 的離心率為
的離心率為![]() ,且焦點(diǎn)到漸近線的距離為
,且焦點(diǎn)到漸近線的距離為![]() .
.
(1)求雙曲線![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若以![]() 為斜率的直線
為斜率的直線![]() 與雙曲線
與雙曲線![]() 相交于兩個不同的點(diǎn)
相交于兩個不同的點(diǎn)![]() ,
,![]() ,且線段
,且線段![]() 的垂直平分線與兩坐標(biāo)軸圍成的三角形的面積為
的垂直平分線與兩坐標(biāo)軸圍成的三角形的面積為![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由焦點(diǎn)到漸近線的距離可求出![]() ,再由離心率求出
,再由離心率求出![]() ,從而得到雙曲線方程;
,從而得到雙曲線方程;
(2)設(shè)直線![]() 的方程為
的方程為![]() ,聯(lián)立
,聯(lián)立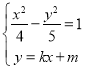 可知
可知![]() ,利用韋達(dá)定理和中點(diǎn)坐標(biāo)公式求出線段
,利用韋達(dá)定理和中點(diǎn)坐標(biāo)公式求出線段![]() 的垂直平分線方程,再利用題設(shè)面積可求出
的垂直平分線方程,再利用題設(shè)面積可求出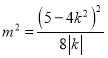 ,結(jié)合
,結(jié)合![]() 即可求出實(shí)數(shù)
即可求出實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
(1)焦點(diǎn)![]() 到漸近線
到漸近線![]() 的距離為
的距離為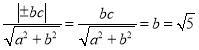 ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴雙曲線![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() .
.
(2)設(shè)直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,
,
則由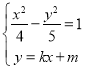 消去
消去![]() ,可得
,可得![]() ,
,
根據(jù)題意可知![]() ,且
,且![]() ,
,
即![]() ①,
①,
設(shè)線段![]() 的中點(diǎn)坐標(biāo)為
的中點(diǎn)坐標(biāo)為![]() ,
,
則![]() ,
,![]() ,
,
∴線段![]() 的垂直平分線方程為
的垂直平分線方程為![]() ,
,
此直線與![]() 軸,
軸,![]() 軸的交點(diǎn)坐標(biāo)分別為
軸的交點(diǎn)坐標(biāo)分別為![]() ,
,![]() ,
,
∴![]() ,化簡可得
,化簡可得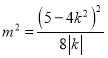 ②,
②,
將②代入①得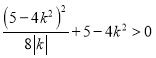 ,
,
即![]() ,解得
,解得![]() 或
或![]() ,
,
∴實(shí)數(shù)![]() 的取值范圍是
的取值范圍是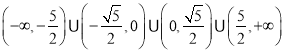 .
.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】高鐵、網(wǎng)購、移動支付和共享單車被譽(yù)為中國的“新四大發(fā)明”,彰顯出中國式創(chuàng)新的強(qiáng)勁活力.某移動支付公司從我市移動支付用戶中隨機(jī)抽取100名進(jìn)行調(diào)查,得到如下數(shù)據(jù):
每周移動支付次數(shù) | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 | 總計 |
男 | 10 | 8 | 7 | 3 | 2 | 15 | 45 |
女 | 5 | 4 | 6 | 4 | 6 | 30 | 55 |
總計 | 15 | 12 | 13 | 7 | 8 | 45 | 100 |
(1)把每周使用移動支付超過3次的用戶稱為“移動支付活躍用戶”,能否在犯錯誤概率不超過0.005的前提下,認(rèn)為是否為“移動支付活躍用戶”與性別有關(guān)?
(2)把每周使用移動支付6次及6次以上的用戶稱為“移動支付達(dá)人”,視頻率為概率,在我市所有“移動支付達(dá)人”中,隨機(jī)抽取4名用戶.
①求抽取的4名用戶中,既有男“移動支付達(dá)人”又有女“移動支付達(dá)人”的概率;
②為了鼓勵男性用戶使用移動支付,對抽出的男“移動支付達(dá)人”每人獎勵300元,記獎勵總金額為X,求X的分布列及均值.
附公式及表如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() :
:![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),曲線
),曲線![]() :
:![]() (
(![]() 為參數(shù)),
為參數(shù)),![]() 與
與![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,以坐標(biāo)原點(diǎn)為極點(diǎn),
,以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系.
軸的非負(fù)半軸為極軸建立極坐標(biāo)系.
(1)求![]() 的極坐標(biāo)方程及點(diǎn)
的極坐標(biāo)方程及點(diǎn)![]() 的極坐標(biāo);
的極坐標(biāo);
(2)已知直線![]() :
:![]() 與圓
與圓![]() :
:![]() 交于
交于![]() ,
,![]() 兩點(diǎn),記
兩點(diǎn),記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
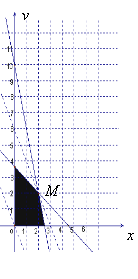
【題目】(本小題滿分13分)某縣一個化肥廠生產(chǎn)甲、乙兩種混合肥料,生產(chǎn)1車皮甲種肥料的主要原料是磷酸鹽4噸、硝酸鹽18噸;生產(chǎn)1車皮乙種肥料需要的主要原料是磷酸鹽1噸、硝酸鹽15噸.先庫存磷酸鹽10噸、硝酸鹽66噸,在此基礎(chǔ)上生產(chǎn)這兩種混合肥料.若生產(chǎn)1車皮甲種肥料產(chǎn)生的利潤為10000元;生產(chǎn)1車皮乙種肥料產(chǎn)生的利潤為5000元.那么分別生產(chǎn)甲、乙兩種肥料各多少車皮能產(chǎn)生最大的利潤?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓離心率為![]() ,且與雙曲線
,且與雙曲線![]() 有相同焦點(diǎn).
有相同焦點(diǎn).
(1)求橢圓標(biāo)準(zhǔn)方程;
(2)過點(diǎn)![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 、
、![]() 兩點(diǎn),原點(diǎn)
兩點(diǎn),原點(diǎn)![]() 在以
在以![]() 為直徑的圓上,求直線
為直徑的圓上,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】車工劉師傅利用數(shù)控車床為某公司加工一種高科技易損零件,對之前加工的100個零件的加工時間進(jìn)行統(tǒng)計,結(jié)果如下:
加工1個零件用時 | 20 | 25 | 30 | 35 |
頻數(shù)(個) | 15 | 30 | 40 | 15 |
以加工這100個零件用時的頻率代替概率.
(1)求![]() 的分布列與數(shù)學(xué)期望
的分布列與數(shù)學(xué)期望![]() ;
;
(2)劉師傅準(zhǔn)備給幾個徒弟做一個加工該零件的講座,用時40分鐘,另外他打算在講座前、講座后各加工1個該零件作示范.求劉師傅講座及加工2個零件作示范的總時間不超過100分鐘的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】第16屆亞運(yùn)會在中國廣州進(jìn)行,為了搞好接待工作,組委會招幕了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,調(diào)查發(fā)現(xiàn),男、女志愿者中分別有
名女志愿者,調(diào)查發(fā)現(xiàn),男、女志愿者中分別有![]() 人和
人和![]() 人喜愛運(yùn)動,其余人不喜愛運(yùn)動.
人喜愛運(yùn)動,其余人不喜愛運(yùn)動.
(1)根據(jù)以上數(shù)據(jù)完成以下![]() 列聯(lián)表:
列聯(lián)表:
喜愛運(yùn)動 | 不喜愛運(yùn)動 | 總計 | |
男 |
|
| |
女 |
|
| |
總計 |
|
(2)根據(jù)列聯(lián)表的獨(dú)立性檢驗(yàn),能否在犯錯誤的概率不超過![]() 的前提下認(rèn)為性別與喜愛運(yùn)動有關(guān)?
的前提下認(rèn)為性別與喜愛運(yùn)動有關(guān)?
附:
|
|
|
|
|
|
|
|
|
|
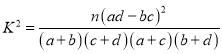 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]() 為橢圓
為橢圓![]() 上的兩點(diǎn),滿足
上的兩點(diǎn),滿足![]() ,其中
,其中![]() ,
,![]() 分別為左右焦點(diǎn).
分別為左右焦點(diǎn).
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,設(shè)直線
,設(shè)直線![]() 的斜率為
的斜率為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,(
,(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出曲線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若射線![]() 與曲線
與曲線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,將
,將![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 后,與曲線
后,與曲線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com