
【題目】2017年5月14日,第一屆“一帶一路”國際高峰論壇在北京舉行,為了解不同年齡的人對“一帶一路”關注程度,某機構隨機抽取了年齡在15-75歲之間的100人進行調查, 經統計“青少年”與“中老年”的人數之比為9:11
關注 | 不關注 | 合計 | |
青少年 | 15 | ||
中老年 | |||
合計 | 50 | 50 | 100 |
(1)根據已知條件完成上面的![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為關注“一帶一路”是否和年齡段有關?
的把握認為關注“一帶一路”是否和年齡段有關?
(2)現從抽取的青少年中采用分層抽樣的辦法選取9人進行問卷調查.在這9人中再選取3人進行面對面詢問,記選取的3人中關注“一帶一路”的人數為X,求X的分布列及數學期望.
附:參考公式 ,其中
,其中![]()
臨界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1) 有![]() 的把握認為關注“一帶一路” 和年齡段有關(2)
的把握認為關注“一帶一路” 和年齡段有關(2) ![]()
【解析】試題分析:(1)依題意完成![]() 列聯表,計算
列聯表,計算![]() ,對照臨界值得出結論;(2)根據分層抽樣法,得出隨機變量
,對照臨界值得出結論;(2)根據分層抽樣法,得出隨機變量![]() 的可能取值,計算對應的概率值,寫出
的可能取值,計算對應的概率值,寫出![]() 的分布列,計算出數學期望值.
的分布列,計算出數學期望值.
試題解析:(1)依題意可知,抽取的“青少年”共有![]() 人,“中老年”共有
人,“中老年”共有![]() 人.
人.
完成的2×2列聯表如:
關注 | 不關注 | 合計 | |
青少年 | 15 | 30 | 45 |
中老年 | 35 | 20 | 55 |
合計 | 50 | 50 | 100 |
則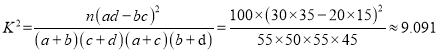
因為![]() ,
, ![]() ,所以有
,所以有![]() 的把握認為關注“一帶一路” 和年齡段有關
的把握認為關注“一帶一路” 和年齡段有關
(2)根據題意知,選出關注的人數為3,不關注的人數為6,在這9人中再選取3人進行面對面詢問, ![]() 的取值可以為0,1,2,3,則
的取值可以為0,1,2,3,則
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() 的分布列為數學期望
的分布列為數學期望![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】下列五個結論:
![]() 集合
集合![]() 2,3,4,5,
2,3,4,5,![]() ,集合
,集合![]() ,若f:
,若f:![]() ,則對應關系f是從集合A到集合B的映射;
,則對應關系f是從集合A到集合B的映射;
![]() 函數
函數![]() 的定義域為
的定義域為![]() ,則函數
,則函數![]() 的定義域也是
的定義域也是![]() ;
;
![]() 存在實數
存在實數![]() ,使得
,使得![]() 成立;
成立;
![]() 是函數
是函數![]() 的對稱軸方程;
的對稱軸方程;
![]() 曲線
曲線![]() 和直線
和直線![]() 的公共點個數為m,則m不可能為1;
的公共點個數為m,則m不可能為1;
其中正確的有______![]() 寫出所有正確的序號
寫出所有正確的序號![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·湖北)某廠用鮮牛奶在某臺設備上生產![]() 兩種奶制品.生產1噸A產品需鮮牛奶2噸,使用設備1小時,獲利1000元;生產1噸B產品需鮮牛奶1.5噸,使用設備1.5小時,獲利1200元.要求每天B產品的產量不超過A產品產量的2倍,設備每天生產
兩種奶制品.生產1噸A產品需鮮牛奶2噸,使用設備1小時,獲利1000元;生產1噸B產品需鮮牛奶1.5噸,使用設備1.5小時,獲利1200元.要求每天B產品的產量不超過A產品產量的2倍,設備每天生產![]() 兩種產品時間之和不超過12小時. 假定每天可獲取的鮮牛奶數量W(單位:噸)是一個隨機變量,其分布列為
兩種產品時間之和不超過12小時. 假定每天可獲取的鮮牛奶數量W(單位:噸)是一個隨機變量,其分布列為
(Ⅰ)求Z的分布列和均值;該廠每天根據獲取的鮮牛奶數量安排生產,使其獲利最大,因此每天的最大獲利Z(單位:元)是一個隨機變量.
(Ⅱ) 若每天可獲取的鮮牛奶數量相互獨立,求3天中至少有1天的最大獲利超過10000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盒中有6只燈泡,其中2只次品,4只正品,有放回地從中任取兩次,每次取一只,試求下列事件的概率:
(1)取到的2只都是次品;
(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 在曲線
在曲線![]() 上,從原點向
上,從原點向![]() 移動,如果直線
移動,如果直線![]() ,曲線
,曲線![]() 及直線
及直線![]() 所圍成的兩個陰影部分的面積分別記為
所圍成的兩個陰影部分的面積分別記為![]() ,
,![]() ,如圖所示.
,如圖所示.
(1)當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(2)當![]() 有最小值時,求點
有最小值時,求點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小張同學計劃在期末考試結束后,和其他小伙伴一塊兒外出旅游,增長見識.旅行社為他們提供了省內的都江堰、峨眉山、九寨溝和省外的麗江古城,黃果樹瀑布和鳳凰古城這六個景點,由于時間和距離等原因,只能從中任取4個景點進行參觀,其中黃果樹瀑布不能第一個參觀,且最后參觀的是省內景點,則不同的旅游順序有( )
A. 54種 B. 72種 C. 120種 D. 144種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓C的參數方程為
中,圓C的參數方程為 ,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線
,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,A,B兩點的極坐標分別為
,A,B兩點的極坐標分別為![]() .
.
(1)求圓C的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)點P是圓C上任一點,求△PAB面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com