觀察下列事實|x|＋|y|＝1的不同整數解(x，y)的個數為4 , |x|＋|y|＝2的不同整數解(x，y)的個數為8, |x|＋|y|＝3的不同整數解(x，y)的個數為12 ….則|x|＋|y|＝20的不同整數解(x，y)的個數為________．
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第七章第3課時練習卷（解析版） 題型：解答題
設函數f(x)＝x－xlnx，數列{an}滿足0＜a1＜1，an＋1＝f(an)．求證：
(1)函數f(x)在區間(0，1)是增函數；
(2)an＜an＋1＜1.
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第七章第2課時練習卷（解析版） 題型：解答題
若實數x、y、m滿足|x－m|＞|y－m|，則稱x比y遠離m.
(1)若x2－1比1遠離0，求x的取值范圍；
(2)對任意兩個不相等的正數a、b，證明：a3＋b3比a2b＋ab2遠離2ab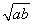
.
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第七章第2課時練習卷（解析版） 題型：填空題
設a、b為兩個正數，且a＋b＝1，則使得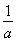
＋
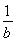≥μ恒成立的μ的取值范圍是________．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第七章第1課時練習卷（解析版） 題型：解答題
設同時滿足條件：①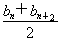
≤bn＋1(n∈N*)；②bn≤M(n∈N*，M是與n無關的常數)的無窮數列{bn}叫“特界” 數列．
(1) 若數列{an}為等差數列，Sn是其前n項和，a3＝4，S3＝18，求Sn；
(2) 判斷(1)中的數列{Sn}是否為“特界” 數列，并說明理由．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第一章第3課時練習卷（解析版） 題型：解答題
設命題p：關于x的不等式2|x－2|<a的解集為?；命題q：函數y＝lg(ax2－x＋a)的值域是R.如果命題p和q有且僅有一個正確，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第一章第2課時練習卷（解析版） 題型：解答題
設集合A＝{x|x2－2x＋2m＋4＝0}，B＝{x|x<0}．若A∩B≠
，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高中數學人教A版選修4-1達標演練模塊檢測練習卷（解析版） 題型：選擇題
如圖所示，四邊形ABCD是⊙O的內接四邊形，延長BC到E，已知∠BCD∶∠ECD＝3∶2，那么∠BOD等于
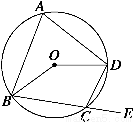
A．120° B．136°
C．144° D．150°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
