
【題目】在平面直角坐標(biāo)系xOy中,已知R為圓![]() 上的一動(dòng)點(diǎn),R在x軸,y軸上的射影分別為點(diǎn)S,T,動(dòng)點(diǎn)P滿(mǎn)足
上的一動(dòng)點(diǎn),R在x軸,y軸上的射影分別為點(diǎn)S,T,動(dòng)點(diǎn)P滿(mǎn)足![]() ,記動(dòng)點(diǎn)P的軌跡為曲線(xiàn)C,曲線(xiàn)C與x軸交于A,B兩點(diǎn).
,記動(dòng)點(diǎn)P的軌跡為曲線(xiàn)C,曲線(xiàn)C與x軸交于A,B兩點(diǎn).
(1)求曲線(xiàn)C的方程;
(2)已知直線(xiàn)AP,BP分別交直線(xiàn)![]() 于點(diǎn)M,N,曲線(xiàn)C在點(diǎn)Р處的切線(xiàn)與線(xiàn)段MN交于點(diǎn)Q,求
于點(diǎn)M,N,曲線(xiàn)C在點(diǎn)Р處的切線(xiàn)與線(xiàn)段MN交于點(diǎn)Q,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)設(shè)![]() ,
,![]() ,根據(jù)已知求出
,根據(jù)已知求出 代入
代入![]() ,即得曲線(xiàn)C的方程;(2)設(shè)
,即得曲線(xiàn)C的方程;(2)設(shè)![]() ,先求出曲線(xiàn)C在點(diǎn)P處的切線(xiàn)方程為
,先求出曲線(xiàn)C在點(diǎn)P處的切線(xiàn)方程為![]() .令
.令![]() ,得點(diǎn)Q的縱坐標(biāo)為
,得點(diǎn)Q的縱坐標(biāo)為![]() ,再根據(jù)
,再根據(jù)![]() 求出
求出![]() 的值.
的值.
(1)設(shè)![]() ,
,![]() ,則
,則![]() ,又R在x軸,y軸上的射影分別為點(diǎn)S,T,
,又R在x軸,y軸上的射影分別為點(diǎn)S,T,
所以![]() ,
,![]() .由
.由![]() ,得
,得 代入
代入![]() ,
,
得![]() ,故曲線(xiàn)C的方程為
,故曲線(xiàn)C的方程為![]() .
.
(2)設(shè)![]() ,則
,則![]() .
.
不妨設(shè)直線(xiàn)AP的方程為![]() ,
,
令![]() ,得點(diǎn)M的縱坐標(biāo)為
,得點(diǎn)M的縱坐標(biāo)為![]() ;直線(xiàn)BP的方程為
;直線(xiàn)BP的方程為![]() ,
,
令![]() ,得點(diǎn)N的縱坐標(biāo)為
,得點(diǎn)N的縱坐標(biāo)為![]() .
.
設(shè)曲線(xiàn)C在點(diǎn)P處的切線(xiàn)方程為![]() ,
,
由 得
得![]() .
.
由![]() ,得
,得![]() ,
,
整理得![]() .
.
將![]() ,
,![]() 代入上式并整理,
代入上式并整理,
得![]() .解得
.解得![]() ,
,
所以曲線(xiàn)C在點(diǎn)P處的切線(xiàn)方程為![]() .
.
令![]() ,得點(diǎn)Q的縱坐標(biāo)為
,得點(diǎn)Q的縱坐標(biāo)為![]() .
.
設(shè)![]() ,所以
,所以![]() ,
,
所以 ,所以
,所以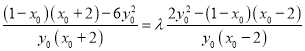
將![]() 代入上式,得
代入上式,得![]() ,
,
解得![]() ,即
,即![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)于不重合的兩個(gè)平面α與β,給定下列條件:
①存在平面γ,使得α,β都平行于γ
②存在兩條不同的直線(xiàn)l,m,使得lβ,mβ,使得l∥α,m∥α
③α內(nèi)有不共線(xiàn)的三點(diǎn)到β的距離相等;
④存在異面直線(xiàn)l,m,使得l∥α,l∥β,m∥α,m∥β.
其中,可以判定α與β平行的條件有( )
A.1個(gè)B.2個(gè)C.3個(gè)D.4個(gè)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】前些年有些地方由于受到提高![]() 的影響,部分企業(yè)只重視經(jīng)濟(jì)效益而沒(méi)有樹(shù)立環(huán)保意識(shí),把大量的污染物排放到空中與地下,嚴(yán)重影響了人們的正常生活,為此政府進(jìn)行強(qiáng)制整治,對(duì)不合格企業(yè)進(jìn)行關(guān)閉,整頓,另一方面進(jìn)行大量的綠化來(lái)凈化和吸附污染物,通過(guò)幾年的整治,環(huán)境明顯得到好轉(zhuǎn),針對(duì)政府這一行為,老百姓大大點(diǎn)贊.
的影響,部分企業(yè)只重視經(jīng)濟(jì)效益而沒(méi)有樹(shù)立環(huán)保意識(shí),把大量的污染物排放到空中與地下,嚴(yán)重影響了人們的正常生活,為此政府進(jìn)行強(qiáng)制整治,對(duì)不合格企業(yè)進(jìn)行關(guān)閉,整頓,另一方面進(jìn)行大量的綠化來(lái)凈化和吸附污染物,通過(guò)幾年的整治,環(huán)境明顯得到好轉(zhuǎn),針對(duì)政府這一行為,老百姓大大點(diǎn)贊.
(1)某機(jī)構(gòu)隨機(jī)訪(fǎng)問(wèn)50名居民,這50名居民對(duì)政府的評(píng)分(滿(mǎn)分100分)如下表:
分?jǐn)?shù) |
|
|
|
|
|
|
頻數(shù) | 2 | 3 | 11 | 14 | 11 | 9 |
請(qǐng)?jiān)诖痤}卡上作出居民對(duì)政府的評(píng)分頻率分布直方圖:
(2)當(dāng)?shù)丨h(huán)保部門(mén)隨機(jī)抽測(cè)了2019年6月的空氣質(zhì)量指數(shù),其數(shù)據(jù)如下表:
空氣質(zhì)量指數(shù) | 0—50 | 50—100 | 100—150 | 150—200 |
天數(shù) | 2 | 18 | 8 | 2 |
用空氣質(zhì)量指數(shù)的平均值作為該月空氣質(zhì)量指數(shù)級(jí)別,求出該月空氣質(zhì)量指數(shù)級(jí)別為第幾級(jí)?(同一組數(shù)據(jù)用該組數(shù)據(jù)的區(qū)間中點(diǎn)值作代表,將頻率視為概率)(相關(guān)知識(shí)參見(jiàn)附表)
(3)空氣受到污染,呼吸系統(tǒng)等疾病患者最易感染,根據(jù)歷史經(jīng)驗(yàn),凡遇到空氣輕度污染,小李每天會(huì)服用有關(guān)藥品花費(fèi)50元,遇到中度污染每天服藥的費(fèi)用達(dá)到100元.環(huán)境整治前的2015年11月份小李因受到空氣污染患呼吸系統(tǒng)等疾病花費(fèi)了5000元,試估計(jì)2019年11月份(參考(2)中表格數(shù)據(jù))小李比以前少花了多少錢(qián)的醫(yī)藥費(fèi)?
附:
空氣質(zhì)量指數(shù) | 0-50 | 50-100 | 100-150 | 150-200 | 200-300 | >300 |
空氣質(zhì)量指數(shù)級(jí)別 | I | II | III | IV | V | VI |
空氣質(zhì)量指數(shù) | 優(yōu) | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴(yán)重污染 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了了解某校學(xué)生課外時(shí)間的分配情況,擬采用分層抽樣的方法從該校的高一、高二、高三這三個(gè)年級(jí)中共抽取5個(gè)班進(jìn)行調(diào)查,已知該校的高一、高二、高三這三個(gè)年級(jí)分別有18、6、6個(gè)班級(jí).
(Ⅰ)求分別從高一、高二、高三這三個(gè)年級(jí)中抽取的班級(jí)個(gè)數(shù);
(Ⅱ)若從抽取的5個(gè)班級(jí)中隨機(jī)抽取2個(gè)班級(jí)進(jìn)行調(diào)查結(jié)果的對(duì)比,求這2個(gè)班級(jí)中至少有1個(gè)班級(jí)來(lái)自高一年級(jí)的概率。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)討論函數(shù)![]() 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 在
在![]() 處取得極大值,求a的取值范圍.
處取得極大值,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2018年12月1日,貴陽(yáng)市地鐵一號(hào)線(xiàn)全線(xiàn)開(kāi)通,在一定程度上緩解了出行的擁堵?tīng)顩r.為了了解市民對(duì)地鐵一號(hào)線(xiàn)開(kāi)通的關(guān)注情況,某調(diào)查機(jī)構(gòu)在地鐵開(kāi)通后的某兩天抽取了部分乘坐地鐵的市民作為樣本,分析其年齡和性別結(jié)構(gòu),并制作出如下等高條形圖:
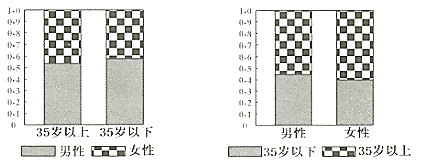
根據(jù)圖中(![]() 歲以上含
歲以上含![]() 歲)的信息,下列結(jié)論中不一定正確的是( )
歲)的信息,下列結(jié)論中不一定正確的是( )
A. 樣本中男性比女性更關(guān)注地鐵一號(hào)線(xiàn)全線(xiàn)開(kāi)通
B. 樣本中多數(shù)女性是![]() 歲以上
歲以上
C. ![]() 歲以下的男性人數(shù)比
歲以下的男性人數(shù)比![]() 歲以上的女性人數(shù)多
歲以上的女性人數(shù)多
D. 樣本中![]() 歲以上的人對(duì)地鐵一號(hào)線(xiàn)的開(kāi)通關(guān)注度更高
歲以上的人對(duì)地鐵一號(hào)線(xiàn)的開(kāi)通關(guān)注度更高
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線(xiàn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 的直線(xiàn)與拋物線(xiàn)交于
的直線(xiàn)與拋物線(xiàn)交于![]() 兩點(diǎn),又過(guò)
兩點(diǎn),又過(guò)![]() 兩點(diǎn)分別作拋物線(xiàn)的切線(xiàn),兩條切線(xiàn)交于
兩點(diǎn)分別作拋物線(xiàn)的切線(xiàn),兩條切線(xiàn)交于![]() 點(diǎn)。
點(diǎn)。
(1)證明:直線(xiàn)![]() 的斜率之積為定值;
的斜率之積為定值;
(2)求![]() 面積的最小值
面積的最小值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)南宋數(shù)學(xué)家楊輝1261年所著的《詳解九章算法》一書(shū)里出現(xiàn)了如圖所示的表,即楊輝三角,這是數(shù)學(xué)史上的一個(gè)偉大成就.在“楊輝三角”中,第![]() 行的所有數(shù)字之和為
行的所有數(shù)字之和為![]() ,若去除所有為1的項(xiàng),依次構(gòu)成數(shù)列
,若去除所有為1的項(xiàng),依次構(gòu)成數(shù)列![]() ,則此數(shù)列的前55項(xiàng)和為( )
,則此數(shù)列的前55項(xiàng)和為( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,圓
中,圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,直線(xiàn)
軸正半軸為極軸建立極坐標(biāo)系,直線(xiàn)![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求圓![]() 的普通方程和直線(xiàn)
的普通方程和直線(xiàn)![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)![]() 是直線(xiàn)
是直線(xiàn)![]() 上任意一點(diǎn),過(guò)
上任意一點(diǎn),過(guò)![]() 作圓
作圓![]() 切線(xiàn),切點(diǎn)為
切線(xiàn),切點(diǎn)為![]() ,
,![]() ,求四邊形
,求四邊形![]() (點(diǎn)
(點(diǎn)![]() 為圓
為圓![]() 的圓心)面積的最小值.
的圓心)面積的最小值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com