
【題目】已知正項等比數列{an}的前n項和為Sn , 且S2=6,S4=30,n∈N* , 數列{bn}滿足bnbn+1=an , b1=1
(1)求an , bn;
(2)求數列{bn}的前n項和為Tn .
【答案】
(1)解:設正項等比數列{an}的公比為q(q>0),
由題意可得a1+a1q=6,a1+a1q+a1q2+a1q3=30,
解得a1=q=2(負的舍去),
可得an=a1qn﹣1=2n;
由bnbn+1=an=2n,b1=1,
可得b2=2,
即有bn+1bn+2=an=2n+1,
可得 ![]() =2,
=2,
可得數列{bn}中奇數項,偶數項均為公比為2的等比數列,
即有bn=  ;
;
(2)解:當n為偶數時,前n項和為Tn=(1+2+..+ ![]() )+(2+4+..+
)+(2+4+..+ ![]() )
)
= ![]() +
+ ![]() =3(
=3( ![]() )n﹣3;
)n﹣3;
當n為奇數時,前n項和為Tn=Tn﹣1+ ![]()
=3( ![]() )n﹣1﹣3+
)n﹣1﹣3+ ![]() =(
=( ![]() )n+3﹣3.
)n+3﹣3.
綜上可得,Tn= ![]()
【解析】(1)設正項等比數列{an}的公比為q(q>0),由等比數列的通項公式,解方程可得首項和公比均為2,可得an=a1qn﹣1=2n;再由n換為n+1,可得數列{bn}中奇數項,偶數項均為公比為2的等比數列,運用等比數列的通項公式,即可得到所求bn;(2)討論n為奇數和偶數,運用分組求和和等比數列的求和公式,化簡整理即可得到所求和.
【考點精析】解答此題的關鍵在于理解數列的前n項和的相關知識,掌握數列{an}的前n項和sn與通項an的關系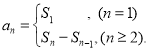 ,以及對數列的通項公式的理解,了解如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
,以及對數列的通項公式的理解,了解如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


科目:高中數學 來源: 題型:
【題目】某校為了了解學生對消防知識的了解情況,從高一年級和高二年級各選取100名同學進行消防知識競賽.下圖(1)和下圖(2)分別是對高一年級和高二年級參加競賽的學生成績按![]() ,
, ![]() ,
, ![]() ,
, ![]() 分組,得到的頻率分布直方圖.
分組,得到的頻率分布直方圖.

(1)請計算高一年級和高二年級成績小于60分的人數;
(2)完成下面![]() 列聯表,并回答:有多大的把握可以認為“學生所在的年級與消防常識的了解存在相關性”?
列聯表,并回答:有多大的把握可以認為“學生所在的年級與消防常識的了解存在相關性”?

附:臨界值表及參考公式:  ,
, ![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() cos(2x-
cos(2x-![]() ).
).
(1)利用“五點法”,完成以下表格,并畫出函數f(x)在一個周期上的圖象;
(2)求函數f(x)的單調遞減區間和對稱中心的坐標;
(3)如何由y=cosx的圖象變換得到f(x)的圖象.
2x- | 0 |
| π |
| 2π |
x | |||||
f(x) |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,面積為![]() 的正方形
的正方形![]() 中有一個不規則的圖形
中有一個不規則的圖形![]() ,可按下面方法估計
,可按下面方法估計![]() 的面積:在正方形
的面積:在正方形![]() 中隨機投擲
中隨機投擲![]() 個點,若
個點,若![]() 個點中有
個點中有![]() 個點落入
個點落入![]() 中,則
中,則![]() 的面積的估計值為
的面積的估計值為![]() ,假設正方形
,假設正方形![]() 的邊長為2,
的邊長為2, ![]() 的面積為1,并向正方形
的面積為1,并向正方形![]() 中隨機投擲
中隨機投擲![]() 個點,以
個點,以![]() 表示落入
表示落入![]() 中的點的數目.
中的點的數目.

(I)求![]() 的均值
的均值![]() ;
;
(II)求用以上方法估計![]() 的面積時,
的面積時, ![]() 的面積的估計值與實際值之差在區間
的面積的估計值與實際值之差在區間![]() 內的概率.
內的概率.
附表: ![]()

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,多面體ABCDEF中,四邊形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于點P 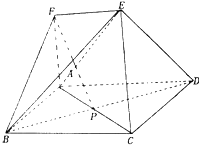
(1)證明:PF∥面ECD;
(2)求二面角B﹣EC﹣A的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,命題
,命題![]() ,
,![]() ;命題
;命題![]() .
.
(1)若![]() 為真命題,求
為真命題,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 為真命題,求
為真命題,求![]() 的取值范圍;
的取值范圍;
(3)若“![]() ”為假命題,“
”為假命題,“![]() ”為假命題,求
”為假命題,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左右焦點分別為
的左右焦點分別為![]() ,
, ![]() ,左頂點為
,左頂點為![]() ,上頂點為
,上頂點為![]() ,
, ![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() :
: ![]() 與橢圓
與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,
, ![]() ,
, ![]() 是線段
是線段![]() 的中點.若經過點
的中點.若經過點![]() 的直線
的直線![]() 與直線
與直線![]() 垂直于點
垂直于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com