【題目】在棱長為2的正方體ABCD﹣A1B1C1D1中，點P是正方體棱上的一點（不包括棱的端點），滿足|PB|+|PD1|= 
的點P的個數為；若滿足|PB|+|PD1|=m的點P的個數為6，則m的取值范圍是 ．
【答案】12；（2 
，2 
）
【解析】解：∵正方體的棱長為2，
∴BD1= 
=2 ，
∵點P是正方體棱上的一點（不包括棱的端點），滿足|PB|+|PD1|= 
，
∴點P是以2c=2 為焦距，以a= 為長半軸，以 
為短半軸的橢圓，
∵P在正方體的棱上，
∴P應是橢圓與正方體與棱的交點，
結合正方體的性質可知，滿足條件的點應該在正方體的12條棱上各有一點滿足條件．
∴滿足|PB|+|PD1|= 的點P的個數為12個．（2）∵滿足|PB|+|PD1|=m的點P的個數為6，
∴|PB|+|PD1|=m＞|BD1|=2 ，∴m＞2 ，
∵正方體的棱長為2，∴正方體的面的對角線的長為2 ，
∵點P的個數為6，∴b＜ ，
∵短半軸長b= 
，∴ 
，解得m＜2 ．
∴m的取值范圍是（2 ，2 ）．
所以答案是：12，（2 ，2 ）．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】某人在如圖所示的直角邊長為4米的三角形地塊的每個格點(指縱、橫直線的交叉點以及三角形的頂點)處都種了一株相同品種的作物．根據歷年的種植經驗，一株該種作物的年收獲量Y(單位：kg)與它的“相近”作物株數X之間的關系如下表所示：
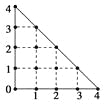
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
這里，兩株作物“相近”是指它們之間的直線距離不超過1米．
(1)從三角形地塊的內部和邊界上分別隨機選取一株作物，求它們恰好“相近”的概率；
(2)從所種作物中隨機選取一株，求它的年收獲量的分布列與數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，以
為極點， 
軸的正半軸為極軸建立極坐標系，直線
的參數方程為
，曲線
的極坐標方程為
.
（1）寫出直線
的直角坐標方程和曲線
的普通方程；
（2）求直線
與曲線
的交點的直角坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若以連續擲兩次骰子分別得到的點數m、n作為點P的坐標（m，n），求：
（1）點P在直線x+y=7上的概率；
（2）點P在圓x2+y2=25外的概率．
（3）將m，n，5的值分別作為三條線段的長，求這三條線段能圍成等腰三角形的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
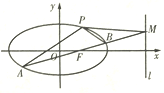
【題目】如圖，橢圓
經過點
，離心率
，直線
的方程為
.
求橢圓
的方程；
是經過右焦點
的任一弦（不經過點
），設直線
與直線
相交于點
，記
， 
， 
的斜率為
， 
， 
.問：是否存在常數
，使得
？若存在，求
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知甲袋中有1個黃球和2個紅球，乙袋中有2個黃球和2個紅球，現隨機地從甲袋中取出兩個球放入乙袋中，然后從乙袋中隨機取出1個球，則從乙袋中取出紅球的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
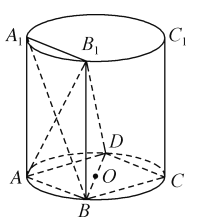
【題目】如圖， 
， 
， 
， 
是圓柱底面圓周的四等分點， 
是圓心， 
， 
， 
與底面
垂直，底面圓的直徑等于圓柱的高．
（1）證明： 
；
（2）求二面角
的大小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
