
【題目】一個盒中裝有編號分別為![]() 的四個形狀大小完全相同的小球.
的四個形狀大小完全相同的小球.
(1)從盒中任取兩球,求取出的球的編號之和大于![]() 的概率.
的概率.
(2)從盒中任取一球,記下該球的編號![]() ,將球放回,再從盒中任取一球,記下該球的編號
,將球放回,再從盒中任取一球,記下該球的編號![]() ,求
,求![]() 的概率.
的概率.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】分析:(1)根據古典概型概率的求解步驟解題即可.(2)結合又放回的取法列舉出所有的基本事件,進而從而得到![]() 包含的事件的個數,由此可得所求的概率.
包含的事件的個數,由此可得所求的概率.
詳解:(1)從盒中任取兩球的所有情況有:
(1,2),(1,3),(1,4)(2,3),(2,4),(3,4),共6種.
其中編號之和大于5的情況有:(2,4),(3,4),共2種,
故編號之和大于5的概率為![]() .
.
(2)有放回的連續取球的所有情況有:
(1,1),(1,2),(1,3),(1,4),
(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2)(3,3),(3,4),
(4,1),(4,2),(4,3),(4,4),共16個.
其中|a﹣b|≥2的包含的情況有:(1,3),(1,4),(2,4),(3,1),(4,1),(4,2),共6個.
所以|a﹣b|≥2的概率為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的兩條漸近線與拋物線y2=2px(p>0)的準線分別交于O、A、B三點,O為坐標原點.若雙曲線的離心率為2,△AOB的面積為
=1(a>0,b>0)的兩條漸近線與拋物線y2=2px(p>0)的準線分別交于O、A、B三點,O為坐標原點.若雙曲線的離心率為2,△AOB的面積為 ![]() ,則p=( )
,則p=( )
A.1
B.![]()
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=x2+bx+c有兩個零點1和﹣1.
(1)求f(x)的解析式;
(2)設g(x)![]() ,試判斷函數g(x)在區間(﹣1,1)上的單調性并用定義證明;
,試判斷函數g(x)在區間(﹣1,1)上的單調性并用定義證明;
(3)由(2)函數g(x)在區間(﹣1,1)上,若實數t滿足g(t﹣1)﹣g(﹣t)>0,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從1,3,5,7,9這五個數中,每次取出兩個不同的數分別記為a,b,共可得到lga﹣lgb的不同值的個數是( )
A.9
B.10
C.18
D.20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只藥用昆蟲的產卵數y與一定范圍內的溫度x有關, 現收集了該種藥用昆蟲的6組觀測數據如下表:
溫度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
產卵數y/個 | 6 | 11 | 20 | 27 | 57 | 77 |
經計算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,線性回歸模型的殘差平方和
,線性回歸模型的殘差平方和![]() ,e8.0605≈3167,其中xi, yi分別為觀測數據中的溫度和產卵數,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分別為觀測數據中的溫度和產卵數,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用線性回歸模型,求y關于x的回歸方程![]() =
=![]() x+
x+![]() (精確到0.1);
(精確到0.1);
(Ⅱ)若用非線性回歸模型求得y關于x的回歸方程為![]() =0.06e0.2303x,且相關指數R2=0.9522.
=0.06e0.2303x,且相關指數R2=0.9522.
( i )試與(Ⅰ)中的回歸模型相比,用R2說明哪種模型的擬合效果更好.
( ii )用擬合效果好的模型預測溫度為35C時該種藥用昆蟲的產卵數(結果取整數).
附:一組數據(x1,y1), (x2,y2), ...,(xn,yn ), 其回歸直線![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估計為
的斜率和截距的最小二乘估計為

![]() =
=![]()
![]() ;相關指數R2=
;相關指數R2= .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某算法的程序框圖如圖所示,其中輸入的變量x在1,2,3,…,24這24個整數中等可能隨機產生
(1)分別求出按程序框圖正確編程運行時輸出y的值為i的概率pi(i=1,2,3);
(2)甲乙兩同學依據自己對程序框圖的理解,各自編程寫出程序重復運行n次后,統計記錄輸出y的值為i(i=1,2,3)的頻數,以下是甲乙所作頻數統計表的部分數據.
甲的頻數統計圖(部分)
運行次數n | 輸出y的值為1的頻數 | 輸出y的值為2的頻數 | 輸出y的值為3的頻數 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的頻數統計圖(部分)
運行次數n | 輸出y的值為1的頻數 | 輸出y的值為2的頻數 | 輸出y的值為3的頻數 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
當n=2100時,根據表中的數據,分別寫出甲、乙所編程序各自輸出y的值為i(i=1,2,3)的頻率(用分數表示),并判斷兩位同學中哪一位所編程序符合要求的可能性較大;
(3)將按程序擺圖正確編寫的程序運行3次,求輸出y的值為2的次數ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設常數a∈R,集合A={x|(x﹣1)(x﹣a)≥0},B={x|x≥a﹣1},若A∪B=R,則a的取值范圍為( )
A.(﹣∞,2)
B.(﹣∞,2]
C.(2,+∞)
D.[2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形區域ABCD的A,C兩點處各有一個通信基站,假設其信號覆蓋范圍分別是扇形區域ADE和扇形區域CBF(該矩形區域內無其他信號來源,基站工作正常).若在該矩形區域內隨機地選一地點,則該地點無信號的概率是( )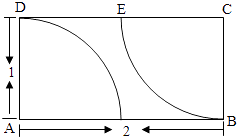
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com