
【題目】某市為了制定合理的節電方案,供電局對居民用電進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:度),將數據按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
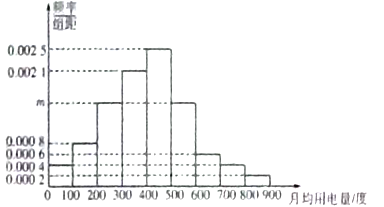
(Ⅰ)求直方圖中![]() 的值并估計居民月均用電量的中位數;
的值并估計居民月均用電量的中位數;
(Ⅱ)現從第8組和第9組的居民中任選取2戶居民進行訪問,則兩組中各有一戶被選中的概率.
【答案】(Ⅰ)![]() .中位數為408度.(Ⅱ)
.中位數為408度.(Ⅱ) ![]() .
.
【解析】試題分析:(1)根據頻率分布直方圖,求解![]() 的值,即可求得前4組的頻率之和,從而估計出居民的月均用電量的中位數;
的值,即可求得前4組的頻率之和,從而估計出居民的月均用電量的中位數;
(2)計算出第8和第9組的戶數,分別設為![]() 和
和![]() ,從而得到選出2戶的基本事件的個數,進而得到兩組中各有一戶被選中的基本事件個數,利用古典概型的概率計算公式,即可求解概率。
,從而得到選出2戶的基本事件的個數,進而得到兩組中各有一戶被選中的基本事件個數,利用古典概型的概率計算公式,即可求解概率。
試題解析:
解:(Ⅰ) ![]() ,
,
∴![]() .
.
設中位數是![]() 度,前5組的頻率之和為
度,前5組的頻率之和為![]() ,
,
而前4組的頻率之和為![]() ,
,
所以![]() ,
, ![]() ,
,
故![]() ,即居民月均用電量的中位數為408度.
,即居民月均用電量的中位數為408度.
(Ⅱ)第8組的戶數為![]() ,分別設為
,分別設為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,第9組的戶數為
,第9組的戶數為![]() ,分別設為
,分別設為![]() ,
, ![]() ,則從中任選出2戶的基本事件為
,則從中任選出2戶的基本事件為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共15種.
共15種.
其中兩組中各有一戶被選中的基本事件為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共8種.
共8種.
所以第8,9組各有一戶被選中的概率![]() .
.


科目:高中數學 來源: 題型:
【題目】某商品的進價為每件![]() 元,售價為每件
元,售價為每件![]() 元,每個月可賣出
元,每個月可賣出![]() 件;如果每件商品在該售價的基礎上每上漲
件;如果每件商品在該售價的基礎上每上漲![]() 元,則每個月少賣
元,則每個月少賣![]() 件(每件售價不能高于
件(每件售價不能高于![]() 元).設每件商品的售價上漲
元).設每件商品的售價上漲![]() 元(
元(![]() 為正整數),每個月的銷售利潤為
為正整數),每個月的銷售利潤為![]() 元.
元.
(1)求![]() 與
與![]() 的函數的函數關系式并直接寫出自變量
的函數的函數關系式并直接寫出自變量![]() 的取值范圍;
的取值范圍;
(2)每件商品的售價定為多少元時,每個月可獲得最大利潤?最大的月利潤是多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過點![]() 作拋物線
作拋物線![]() 的兩條切線, 切點分別為
的兩條切線, 切點分別為![]() ,
, ![]() .
.
(1) 證明: ![]() 為定值;
為定值;
(2) 記△![]() 的外接圓的圓心為點
的外接圓的圓心為點![]() , 點
, 點![]() 是拋物線
是拋物線![]() 的焦點, 對任意實數
的焦點, 對任意實數![]() , 試判斷以
, 試判斷以![]() 為直徑的圓是否恒過點
為直徑的圓是否恒過點![]() ? 并說明理由.
? 并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一種新型的洗衣液,去污速度特別快.已知每投放k(1≤k≤4,且k∈R)個單位的洗衣液在一定量水的洗衣機中,它在水中釋放的濃度y(克/升)隨著時間x(分鐘)變化的函數關系式近似為y=k·f(x),其中f(x)=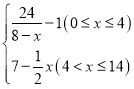 若多次投放,則某一時刻水中的洗衣液濃度為每次投放的洗衣液在相應時刻所釋放的濃度之和.根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起到有效去污的作用.
若多次投放,則某一時刻水中的洗衣液濃度為每次投放的洗衣液在相應時刻所釋放的濃度之和.根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起到有效去污的作用.
(1)若只投放一次k個單位的洗衣液,兩分鐘時水中洗衣液的濃度為3(克/升),求k的值;
(2)若只投放一次4個單位的洗衣液,則有效去污時間可達幾分鐘?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=2sin(x-![]() )-
)-![]() ,現將f(x)的圖象向左平移
,現將f(x)的圖象向左平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度,得到函數g(x)的圖象.
個單位長度,得到函數g(x)的圖象.
(1)求f(![]() )+g(
)+g(![]() )的值;
)的值;
(2)若a,b,c分別是△ABC三個內角A,B,C的對邊,a+c=4,且當x=B時,g(x)取得最大值,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知長方體ABCD-A1B1C1D1的對稱中心在坐標原點,交于同一頂點的三個面分別平行于三個坐標平面,頂點A(-2,-3,-1),求其他七個頂點的坐標.
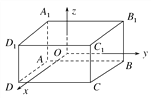
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知直線方程為(2+m)x+(1-2m)y+4-3m=0,求證:不論m為何實數,此直線必過定點;
(2)過這定點引一直線,使它夾在兩坐標軸間的線段被這點平分,求這條直線的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com