(本小題共14分)
如圖,在四棱錐

中,


平面

,底面

是菱形,

.

(Ⅰ)求證:

平面
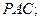
(Ⅱ)若

求

與
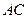
所成角的余弦值;
(Ⅲ)當(dāng)平面

與平面

垂直時,求

的長.
:證明:(Ⅰ)因為四邊形ABCD是菱形,所以

又因為

平面

。所以

,
所以

平面

。
(Ⅱ)

設(shè)

,因為

所以

,如圖,以O(shè)為坐標原點,建立空間直角坐標系

,則

所

設(shè)

與
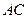
所成角為

,則


(Ⅲ)由(Ⅱ)知

設(shè)


。則

設(shè)平面

的法
向量

則

,所以

令

則


,
所以

同理,平面

的法向量


,因為平面


,所以

,即

解得

,所以


練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,圓

與圓

內(nèi)切于點

,其半徑分別為

與

,圓

的弦

交圓

于點

(

不在

上),求證:

為定值。

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
選修4-1:幾何證明選講
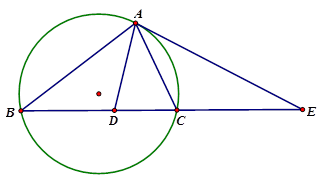
如圖所示,設(shè)
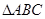
的外接圓的切線
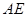
與
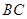
的延長線交于點
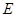
,
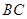
邊上有一點
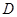
,滿足
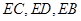
組成等比數(shù)列。求證:
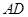
平分
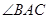
。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
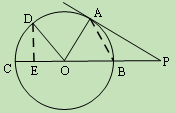
如圖,
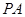
切圓
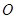
于點
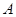
,割線
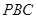
經(jīng)過圓心
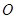
,
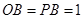
,
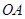
繞點
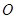
逆時針旋轉(zhuǎn)
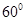
到
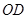
,則
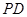
的長為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
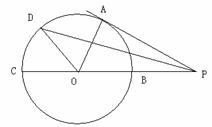
選修4—1:幾何證明選講。如圖,PA切圓O于點A,割線PBC經(jīng)過圓心O,
OB=PB=1,OA繞點O逆時針旋轉(zhuǎn)
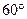
到OD.
(1)求線段PD的長;
(2)在如圖所示的圖形中是否有長度為
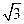
的線段?若有,指出該線段;若沒有,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
在

中,

分別為

上的點,且

,

的面積是

,梯形

的面積為

,則

的值為( )
A.
 B
B.
 C
C.
 D
D.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分10分)選修4-1:幾何證明選講
如圖,已知
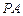
與圓
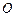
相切于點
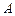
,半徑
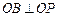
,
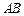
交
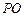
于點
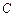
.
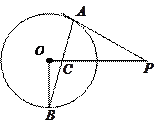
(Ⅰ)求證:
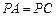
;
(Ⅱ)若圓
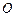
的半徑為3,
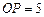
,求
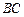
的長度.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
(幾何證明選講選做題)如圖所示,AC和AB分別是圓O的切線,B、C 為切點,且OC = 3,AB = 4,延長AO到D點,則△ABD的面積是___________.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
(幾何證明選做題)如圖,已知:△
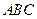
內(nèi)接于

圓
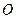
,
點
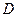
在
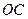

的延長線上,
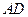
是圓
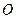
的切線,若
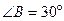
,
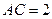
,則
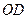
的長為
.
查看答案和解析>>

 中,
中,
 平面
平面 ,底面
,底面 是菱形,
是菱形, .
.
 平面
平面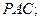
 求
求 與
與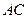 所成角的余弦值;
所成角的余弦值; 與平面
與平面 垂直時,求
垂直時,求 的長.
的長.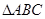 的外接圓的切線
的外接圓的切線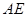 與
與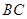 的延長線交于點
的延長線交于點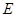 ,
,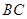 邊上有一點
邊上有一點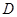 ,滿足
,滿足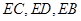 組成等比數(shù)列。求證:
組成等比數(shù)列。求證: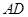 平分
平分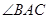 。
。
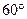 到OD.
到OD.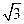 的線段?若有,指出該線段;若沒有,說明理由.
的線段?若有,指出該線段;若沒有,說明理由.
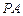 與圓
與圓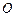 相切于點
相切于點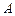 ,半徑
,半徑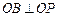 ,
,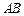 交
交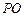 于點
于點 .
.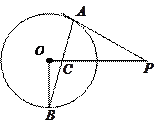
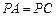 ;
; 的半徑為3,
的半徑為3,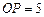 ,求
,求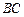 的長度.
的長度.