【題目】已知函數
，
是常數．
（Ⅰ）求曲線
在點
處的切線方程，并證明對任意，切線經過定點；
（Ⅱ）當
時，設
，
是
的兩個正的零點，求證：
．
科目：高中數學 來源： 題型：
【題目】平面直角坐標系xOy中，F(-1, 0)是橢圓
的左焦點，過點F且方向向量為
的光線，經直線
反射后通過左頂點D
.
(I)求橢圓
的方程;
(II)過點F作斜率為
的直線
交橢圓
于A, B兩點，M為AB的中點，直線OM (0為原點)與直線
交于點P，若滿足
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《數書九章》三斜求積術：“以小斜冪，并大斜冪，減中斜冪，余半之，自乘于上；以小斜冪乘大斜冪，減上，余四約一，為實，一為從隅，開平方得積”.秦九韶把三角形的三條邊分別稱為小斜、中斜和大斜，“術”即方法.以
， 
， 
， 
分別表示三角形的面積，大斜，中斜，小斜； 
， 
， 
分別為對應的大斜，中斜，小斜上的高；則
.若在
中
， 
， 
，根據上述公式，可以推出該三角形外接圓的半徑為__________．
【答案】
【解析】根據題意可知： 
，故設
，由
代入
可得
，由余弦定理可得cosA=
，所以由正弦定理得三角形外接圓半徑為
【題型】填空題
【結束】
17
【題目】在等差數列
中，已知公差
， 
，且
， 
， 
成等比數列.
（1）求數列
的通項公式
；
（2）求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
（
）經過點
，且兩焦點與短軸的一個端點的連線構成等腰直角三角形.
（1）求橢圓的方程；
（2）動直線
： 
（
， 
）交橢圓
于
、
兩點，試問：在坐標平面上是否存在一個定點
，使得以
為直徑的圓恒過點
.若存在，求出點
的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
的極坐標方程是
，以極點為原點，極軸為
軸正方向建立平面直角坐標系，曲線
的參數方程是
（
為參數）．
（Ⅰ）將曲線的參數方程化為普通方程；
（Ⅱ）求曲線與曲線交點的極坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面直角坐標系xOy中，F(-1, 0)是橢圓
的左焦點，過點F且方向向量為
的光線，經直線
反射后通過左頂點D
.
(I)求橢圓
的方程;
(II)過點F作斜率為
的直線
交橢圓
于A, B兩點，M為AB的中點，直線OM (0為原點)與直線
交于點P，若滿足
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
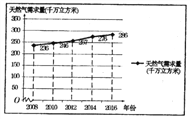
【題目】2017年12月，針對國內天然氣供應緊張的問題，某市政府及時安排部署，加氣站采取了緊急限氣措施，全市居民打響了節約能源的攻堅戰.某研究人員為了了解天然氣的需求狀況，對該地區某些年份天然氣需求量進行了統計，并繪制了相應的折線圖.
（Ⅰ）由折線圖可以看出，可用線性回歸模型擬合年度天然氣需求量
(單位：千萬立方米)與年份
(單位：年)之間的關系.并且已知關于的線性回歸方程是
，試確定
的值，并預測2018年該地區的天然氣需求量；
（Ⅱ）政府部門為節約能源出臺了《購置新能源汽車補貼方案》，該方案對新能源汽車的續航里程做出了嚴格規定，根據續航里程的不同，將補貼金額劃分為三類，A類：每車補貼1萬元，B類：每車補貼2.5萬元，C類：每車補貼3.4萬元.某出租車公司對該公司60輛新能源汽車的補貼情況進行了統計，結果如下表：
為了制定更合理的補貼方案，政府部門決定利用分層抽樣的方式了解出租車公司新能源汽車的補貼情況，在該出租車公司的60輛車中抽取6輛車作為樣本，再從6輛車中抽取2輛車進一步跟蹤調查，求恰好有1輛車享受3.4萬元補貼的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l1：3x－2y－1＝0，直線l2：ax－by＋1＝0，其中a，b∈{1,2,3,4,5,6}．
(1)求直線l1∩l2≠的概率；
(2)求直線l1與l2的交點位于第一象限的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
