
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為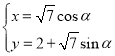 (
(![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和
的極坐標方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)直線![]() 與曲線
與曲線![]() ,
,![]() 分別交于第一象限內
分別交于第一象限內![]() ,
,![]() 兩點,求
兩點,求![]() .
.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】為實現(xiàn)有效利用扶貧資金,增加貧困村民的收入,扶貧工作組結合某貧困村水質優(yōu)良的特點,決定利用扶貧資金從外地購買甲、乙、丙三種魚苗在魚塘中進行養(yǎng)殖試驗,試驗后選擇其中一種進行大面積養(yǎng)殖,已知魚苗甲的自然成活率為0.8.魚苗乙,丙的自然成活率均為0.9,且甲、乙、丙三種魚苗是否成活相互獨立.
(1)試驗時從甲、乙,丙三種魚苗中各取一尾,記自然成活的尾數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學期望;
的分布列和數(shù)學期望;
(2)試驗后發(fā)現(xiàn)乙種魚苗較好,扶貧工作組決定購買![]() 尾乙種魚苗進行大面積養(yǎng)殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產(chǎn)生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
尾乙種魚苗進行大面積養(yǎng)殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產(chǎn)生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“黃梅時節(jié)家家雨”“梅雨如煙暝村樹”“梅雨暫收斜照明”…江南梅雨的點點滴滴都流露著濃烈的詩情.每年六、七月份,我國長江中下游地區(qū)進入持續(xù)25天左右的梅雨季節(jié),如圖是江南![]() 鎮(zhèn)2009~2018年梅雨季節(jié)的降雨量(單位:
鎮(zhèn)2009~2018年梅雨季節(jié)的降雨量(單位:![]() )的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:
)的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:

(1)計算![]() 的值,并用樣本平均數(shù)估計
的值,并用樣本平均數(shù)估計![]() 鎮(zhèn)明年梅雨季節(jié)的降雨量;
鎮(zhèn)明年梅雨季節(jié)的降雨量;
(2)![]() 鎮(zhèn)的楊梅種植戶老李也在犯愁,他過去種植的甲品種楊梅,畝產(chǎn)量受降雨量的影響較大(把握超過八成).而乙品種楊梅這10年的畝產(chǎn)量(
鎮(zhèn)的楊梅種植戶老李也在犯愁,他過去種植的甲品種楊梅,畝產(chǎn)量受降雨量的影響較大(把握超過八成).而乙品種楊梅這10年的畝產(chǎn)量(![]() /畝)與降雨量的發(fā)生頻數(shù)(年)如
/畝)與降雨量的發(fā)生頻數(shù)(年)如![]() 列聯(lián)表所示(部分數(shù)據(jù)缺失).請你完善
列聯(lián)表所示(部分數(shù)據(jù)缺失).請你完善![]() 列聯(lián)表,幫助老李排解憂愁,試想來年應種植哪個品種的楊梅受降雨量影響更小?并說明理由.
列聯(lián)表,幫助老李排解憂愁,試想來年應種植哪個品種的楊梅受降雨量影響更小?并說明理由.
畝產(chǎn)量\降雨量 | 200~400之間 | 200~400之外 | 合計 |
| 2 | ||
| 1 | ||
合計 | 10 |
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.703 |
(參考公式:![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直,求實數(shù)a的值;
垂直,求實數(shù)a的值;
(2)若函數(shù)![]() 在
在![]() 上單調遞增,求實數(shù)a的取值范圍;
上單調遞增,求實數(shù)a的取值范圍;
(3)當![]() 時,若方程
時,若方程![]() 有兩個相異實根
有兩個相異實根![]() ,
,![]() ,
,![]() ,求證
,求證![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,其焦距為
,其焦距為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,
上,![]() ,直線
,直線![]() 的斜率為
的斜率為![]() (
(![]() 為半焦距)·
為半焦距)·
(1)求橢圓![]() 的方程;
的方程;
(2)設圓![]() 的切線
的切線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(
兩點(![]() 為坐標原點),求證:
為坐標原點),求證:![]() ;
;
(3)在(2)的條件下,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4一4:坐標系與參數(shù)方程
在平面直角坐標系xOy中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() 參數(shù)),以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線
參數(shù)),以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線![]() 是圓心的極坐標為(
是圓心的極坐標為(![]() )且經(jīng)過極點的圓
)且經(jīng)過極點的圓
(1)求曲線C1的極坐標方程和C2的普通方程;
(2)已知射線![]() 分別與曲線C1,C2交于點A,B(點B異于坐標原點O),求線段AB的長
分別與曲線C1,C2交于點A,B(點B異于坐標原點O),求線段AB的長
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】針對時下的“抖音熱”某校團委對“學生性別和喜歡抖音是否有關”作了一次調查,其中被調查的男女生人數(shù)相同,男生喜歡抖音的人數(shù)占男生人數(shù)的![]() ,女生喜歡抖音的人數(shù)占女生人數(shù)
,女生喜歡抖音的人數(shù)占女生人數(shù)![]() ,若有
,若有![]() 的把握認為是否喜歡抖音和性別有關則調查人數(shù)中男生可能有( )人
的把握認為是否喜歡抖音和性別有關則調查人數(shù)中男生可能有( )人
附表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附:
A.20B.40C.60D.80
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,點
為平行四邊形,點![]() 在面
在面![]() 內的射影為
內的射影為![]() ,
,![]() ,點
,點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,且直線
,且直線![]() 與
與![]() 垂直.
垂直.
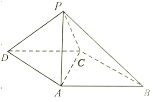
(Ⅰ)在棱![]() 上找一點
上找一點![]() ,使直線
,使直線![]() 與平面
與平面![]() 平行,并說明理由;
平行,并說明理由;
(Ⅱ)在(Ⅰ)的條件下,求二面角![]() 的大小.
的大小.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com