
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��֪����![]() ��ƽ��ֱ������(bi��o)ϵ
��ƽ��ֱ������(bi��o)ϵ![]() �µą���(sh��)���̞�
�µą���(sh��)���̞� ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)
�酢��(sh��)����������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)����
��O�c(di��n)����![]() �S�����S��O�S�������O����(bi��o)ϵ��
�S�����S��O�S�������O����(bi��o)ϵ��
��1��������![]() ����ͨ���̼��O����(bi��o)���̣�
����ͨ���̼��O����(bi��o)���̣�
��2��ֱ��![]() �ĘO����(bi��o)������
�ĘO����(bi��o)������![]() ���侀
���侀![]() ��
�� ![]() �c����
�c����![]() �����c(di��n)
�����c(di��n)![]() �cֱ��
�cֱ��![]() �����c(di��n)
�����c(di��n)![]() ����
����![]() ���L(zh��ng)��
���L(zh��ng)��
���𰸡���1��![]() ��
�� ![]() ����2��
����2��![]() .
.
��������ԇ�}��������1������![]() ����ȥ����(sh��)����(j��ng)�A�ą���(sh��)���̻�����ͨ����.��
����ȥ����(sh��)����(j��ng)�A�ą���(sh��)���̻�����ͨ����.��![]() ���Ɍ��A����ͨ���̻���O����(bi��o)����.��2����
���Ɍ��A����ͨ���̻���O����(bi��o)����.��2����![]() �քe����ֱ���ĘO����(bi��o)���̺͈A�ĘO����(bi��o)���̣������
�քe����ֱ���ĘO����(bi��o)���̺͈A�ĘO����(bi��o)���̣������![]() ���c(di��n)��(du��)��(y��ng)��
���c(di��n)��(du��)��(y��ng)��![]() ��ֵ��������������
��ֵ��������������![]() ���L(zh��ng).
���L(zh��ng).
ԇ�}��������1����?y��n)�����![]() �ą���(sh��)���̞�
�ą���(sh��)���̞� ��
��![]() �酢��(sh��)����
�酢��(sh��)����
��ȥ����(sh��)![]() ������
������![]() ����ͨ���̞�
����ͨ���̞�![]() ��
��
��![]() ��
�� ![]() ��
��
������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��2���� ��
��
���侀![]() �c����
�c����![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() �ĘO����(bi��o)��
�ĘO����(bi��o)��![]() ��
��
��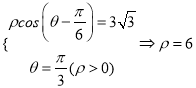 ��
��
���侀![]() �cֱ��
�cֱ��![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() �ĘO����(bi��o)��
�ĘO����(bi��o)��![]() ��
��
��![]() .
.


 ��x��܇(ch��)ϵ�д�
��x��܇(ch��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������w![]() �У�
�У� ![]() �քe��
�քe��![]() �����c(di��n)��
�����c(di��n)��
��1���C����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ����һ�c(di��n)
����һ�c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����2015�߿��Ĵ�����21����֪����(sh��)f(x)����2lnx��x2��2ax��a2������a>0.
(��)�O(sh��)g(x)��f(x)�Č�(d��o)����(sh��)��ӑՓg(x)�Ć��{(di��o)�ԣ�
(��)�C��������a��(0��1)��ʹ��f(x)��0���������f(x)��0�څ^(q��)�g(1������)��(n��i)��Ψһ��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���������q�~(y��)ÿ�궼Ҫ�������ϣ��λخa(ch��n)�خa(ch��n)��.ӛ�q�~(y��)�����ٞ�![]() ���q�~(y��)�ĺ������Ć�λ��(sh��)��
���q�~(y��)�ĺ������Ć�λ��(sh��)��![]() ���о��аl(f��)�F(xi��n)
���о��аl(f��)�F(xi��n)![]() �c
�c![]() �����ȣ��Ү�(d��ng)
�����ȣ��Ү�(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ��
��
��1�����![]() �P(gu��n)��
�P(gu��n)��![]() �ĺ���(sh��)����ʽ��
�ĺ���(sh��)����ʽ��
��2��Ӌ(j��)��һ�l�q�~(y��)��������![]() �r(sh��)�������Ć�λ��(sh��)��
�r(sh��)�������Ć�λ��(sh��)��
��3����(d��ng)�q�~(y��)����������![]() �r(sh��)�����������ԭ��(l��i)�Ďױ���
�r(sh��)�����������ԭ��(l��i)�Ďױ���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(qi��ng)�U(xi��n)��܇(ch��)����횞�C(j��)��(d��ng)܇(ch��)ُ(g��u)�I(m��i)���U(xi��n)�N������ͨ6������˽��܇(ch��)Ͷ������(qi��ng)�U(xi��n)��һ����M(f��i)�ã�����(zh��n)���M(f��i)���y(t��ng)һ��![]() Ԫ������һ���m(x��)���r(sh��)����(sh��)�е����M(f��i)�ʸ���(d��ng)�C(j��)�ƣ����M(f��i)�c��һ���܇(ch��)�v�l(f��)����·��ͨ�¹ʵ���r��(li��n)ϵ���l(f��)����ͨ�¹ʵĴΔ�(sh��)Խ�࣬�M(f��i)��Ҳ����Խ�ߣ����w����(d��ng)��r���±���
Ԫ������һ���m(x��)���r(sh��)����(sh��)�е����M(f��i)�ʸ���(d��ng)�C(j��)�ƣ����M(f��i)�c��һ���܇(ch��)�v�l(f��)����·��ͨ�¹ʵ���r��(li��n)ϵ���l(f��)����ͨ�¹ʵĴΔ�(sh��)Խ�࣬�M(f��i)��Ҳ����Խ�ߣ����w����(d��ng)��r���±���
����(qi��ng)�U(xi��n)����(d��ng)���غ���(d��ng)�M(f��i)�ʱ��ʱ� | ||
����(d��ng)���� | ����(d��ng)���� | |
| ��һ��(g��)���δ�l(f��)����؟(z��)�ε�·��ͨ�¹� | �¸�10% |
| �σɂ�(g��)���δ�l(f��)����؟(z��)�ε�·��ͨ�¹� | �¸�20% |
| ������(g��)���������δ�l(f��)����؟(z��)�ε�·��ͨ�¹� | �¸�30% |
| ��һ��(g��)��Ȱl(f��)��һ����؟(z��)�β��漰�����ĵ�·��ͨ�¹� | 0% |
| ��һ��(g��)��Ȱl(f��)���ɴμ��ɴ�������؟(z��)�ε�·��ͨ�¹� | �ϸ�10% |
| ��һ��(g��)��Ȱl(f��)����؟(z��)�ε�·��ͨ�����¹� | �ϸ�30% |
ij�C(j��)��(g��u)���� ijһƷ����ͨ6������˽��܇(ch��)��Ͷ����r���S�C(j��)��ȡ��60�v܇(ch��)�g�ѝM�����ԓƷ��ͬ��̖(h��o)˽��܇(ch��)����һ���m(x��)���r(sh��)����r���y(t��ng)Ӌ(j��)�õ�������ı���
�(l��i)�� |
|
|
|
|
|
|
��(sh��)�� | 10 | 5 | 5 | 20 | 15 | 5 |
���@60�vԓƷ��܇(ch��)��Ͷ���(l��i)�͵��l�ʴ���һ�v܇(ch��)Ͷ���(l��i)�͵ĸ��ʣ�������І�(w��n)�}��
��1�������҇�(gu��)���C(j��)��(d��ng)܇(ch��)��ͨ�¹�؟(z��)�Ώ�(qi��ng)�Ʊ��U(xi��n)�l������܇(ch��)����(qi��ng)�U(xi��n)�r(ji��)���Ҏ(gu��)���� ![]() ��ӛ
��ӛ![]() ��ijͬ�W(xu��)�ҵ�һ�vԓƷ��܇(ch��)�ڵ������m(x��)���r(sh��)���M(f��i)�ã���
��ijͬ�W(xu��)�ҵ�һ�vԓƷ��܇(ch��)�ڵ������m(x��)���r(sh��)���M(f��i)�ã���![]() �ķֲ����c��(sh��)�W(xu��)����������(sh��)�W(xu��)����ֵ��������(g��)λ��(sh��)�֣�
�ķֲ����c��(sh��)�W(xu��)����������(sh��)�W(xu��)����ֵ��������(g��)λ��(sh��)�֣�
��2��ij����܇(ch��)�N(xi��o)���̌�(zhu��n)�T(m��n)�N(xi��o)���@һƷ�ƵĶ���܇(ch��)���Ҍ���һ��Ľ���(qi��ng)�U(xi��n)���M(f��i)���ڻ������M(f��i)��܇(ch��)�vӛ���¹�܇(ch��)�����O(sh��)ُ(g��u)�M(j��n)һ�v�¹�܇(ch��)̝�p5000Ԫ��һ�v���¹�܇(ch��)ӯ��10000Ԫ��
����ԓ�N(xi��o)����ُ(g��u)�M(j��n)���v��܇(ch��)�g�ѝM���꣩ԓƷ�ƶ���܇(ch��)�����@���v܇(ch��)��������һ�v�¹�܇(ch��)�ĸ��ʣ�
����ԓ�N(xi��o)����һ��ُ(g��u)�M(j��n)100�v��܇(ch��)�g�ѝM���꣩ԓƷ�ƶ���܇(ch��)�������@������(r��n)������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
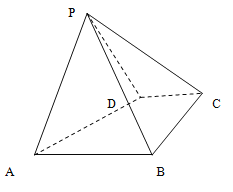
���}Ŀ����D�������F![]() �У�����
�У�����![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() ,
,![]() ��
��![]() ,��(c��)��
,��(c��)��![]() ����
����![]() ,��
,��![]() ����
����![]() ��ĵ���������.
��ĵ���������.
�������C����![]()
�������������F![]() ���w�e����
���w�e����![]() .��(w��n)���Ƿ�����^(gu��)�c(di��n)
.��(w��n)���Ƿ�����^(gu��)�c(di��n)![]() ��ƽ��
��ƽ��![]() �քe��
�քe��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��ʹ��ƽ��
��ʹ��ƽ��![]() ƽ��
ƽ��![]() �������ڣ����
�������ڣ����![]() ����e���������ڣ�Ո(q��ng)�f(shu��)������.
����e���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ֪��![]() �c�AC��
�c�AC��![]() �ཻ��A��B���c(di��n)����AB���c(di��n)��M��0��1����
�ཻ��A��B���c(di��n)����AB���c(di��n)��M��0��1����
��1����(sh��)��(sh��)![]() ��ȡֵ�����Լ�ֱ��
��ȡֵ�����Լ�ֱ��![]() �ķ��̣�
�ķ��̣�
��2����AC�ϴ����Ă�(g��)�c(di��n)��ֱ��![]() �ľ��x��
�ľ��x��![]() ����(sh��)��(sh��)a��ȡֵ������
����(sh��)��(sh��)a��ȡֵ������
��3����֪N��0����3������AC�ϴ��ڃɂ�(g��)��ͬ���c(di��n)P��ʹ![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]()
.
��1����![]()
��![]()
̎���о����̣�
��2����![]()
����![]()
���{(di��o)�^(q��)�g��
��3��������![]()
��![]()
������![]()
���������(sh��)��(sh��)![]()
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������x��R�ϵĺ���(sh��)![]() �M��
�M��![]() ���Ү�(d��ng)
���Ү�(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ���t����(sh��)
���t����(sh��)![]() �څ^(q��)�g[-7,1]�ϵ����c(di��n)��(g��)��(sh��)��( )
�څ^(q��)�g[-7,1]�ϵ����c(di��n)��(g��)��(sh��)��( )
A. 4 B. 6 C. 8 D. 10
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com