
【題目】對于函數![]() ,有下列五個命題:
,有下列五個命題:
①若![]() 存在反函數,且與反函數圖象有公共點,則公共點一定在直線
存在反函數,且與反函數圖象有公共點,則公共點一定在直線![]() 上;
上;
②若![]() 在
在![]() 上有定義,則
上有定義,則![]() 一定是偶函數;
一定是偶函數;
③若![]() 是偶函數,且
是偶函數,且![]() 有解,則解的個數一定是偶數;
有解,則解的個數一定是偶數;
④若![]() 是函數
是函數![]() 的周期,則
的周期,則![]() ,也是函數
,也是函數![]() 的周期;
的周期;
⑤![]() 是函數
是函數![]() 為奇函數的充分不必要條件。
為奇函數的充分不必要條件。
從中任意抽取一個,恰好是真命題的概率為 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
①若y=f(x)存在反函數,且與反函數圖象有公共點,則公共點不一定在直線y=x上,如函數f(x)=![]() ,反函數是其本身,公共點是整個函數圖象;
,反函數是其本身,公共點是整個函數圖象;
②若y=f(x)在R上有定義,則y=f(|x|)一定是偶函數,因f(|-x|)=f(|x|)對于任意x恒成立,故正確;
③若y=f(x)是偶函數,且f(x)=0有解,則解的個數一定是偶數不正確,如y=x2,是偶函數,x2=0的解只有一個,不是偶數個;
④若T(T≠0)是函數y=f(x)的周期,則f(x+T)=f(x),從而f(x+nT)=f(x),則nT(n∈N),也是函數y=f(x)的周期;
⑤f(0)=0是函數y=f(x)為奇函數的充分也不必要條件,不正確,f(x)=x2時,f(0)=0,而f(x)=x2是偶函數.
故正確的命題有2個,
則從中任意抽取一個,恰好是真命題的概率為![]()
故選B.


科目:高中數學 來源: 題型:
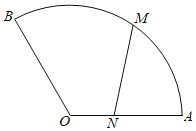
【題目】某公園草坪上有一扇形小徑(如圖),扇形半徑為![]() ,中心角為
,中心角為![]() ,甲由扇形中心
,甲由扇形中心![]() 出發沿
出發沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同時乙從
快走,同時乙從![]() 出發,沿扇形弧以每秒
出發,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,記
慢跑,記![]() 秒時甲、乙兩人所在位置分別為
秒時甲、乙兩人所在位置分別為![]() ,
,![]() ,通過計算
,通過計算![]() ,判斷下列說法是否正確:
,判斷下列說法是否正確:
(1)當![]() 時,函數
時,函數![]() 取最小值;
取最小值;
(2)函數![]() 在區間
在區間![]() 上是增函數;
上是增函數;
(3)若![]() 最小,則
最小,則![]() ;
;
(4)![]() 在
在![]() 上至少有兩個零點;
上至少有兩個零點;
其中正確的判斷序號是______(把你認為正確的判斷序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為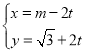 (
(![]() ,
,![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為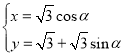 (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,求曲線
軸正半軸為極軸建立極坐標系,求曲線![]() 的極坐標方程;
的極坐標方程;
(2)若![]() ,點
,點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,定義![]() 為兩點
為兩點![]() 、
、![]() 的“切比雪夫距離”,又設點
的“切比雪夫距離”,又設點![]() 及
及![]() 上任意一點
上任意一點![]() ,稱
,稱![]() 的最小值為點
的最小值為點![]() 到直線
到直線![]() 的“切比雪夫距離”,記作
的“切比雪夫距離”,記作![]() ,給出四個命題,正確的是________.
,給出四個命題,正確的是________.
①對任意三點![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
② 到原點的“切比雪夫距離”等于![]() 的點的軌跡是正方形;
的點的軌跡是正方形;
③ 已知點![]() 和直線
和直線![]() ,則
,則![]() ;
;
④ 定點![]() 、
、![]() ,動點
,動點![]() 滿足
滿足![]() ,則點
,則點![]() 的軌跡與直線
的軌跡與直線![]() (
(![]() 為常數)有且僅有
為常數)有且僅有![]() 個公共點.
個公共點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 、
、![]() 、
、![]() 是同一平面上不共線的四點,若存在一組正實數
是同一平面上不共線的四點,若存在一組正實數![]() 、
、![]() 、
、![]() ,使得
,使得![]() ,則三個角
,則三個角![]() 、
、![]() 、
、![]() ( )
( )
A. 都是鈍角B. 至少有兩個鈍角
C. 恰有兩個鈍角D. 至多有兩個鈍角
查看答案和解析>>
科目:高中數學 來源: 題型:
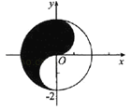
【題目】太極圖被稱為“中華第一圖”.從孔廟大成殿梁柱,到樓觀臺、三茅宮標記物;從道袍、卦攤、中醫、氣功、武術到韓國國旗![]() ,太極圖無不躍居其上.這種廣為人知的太極圖,其形狀如陰陽兩魚互抱在一起,因而被稱為“陰陽魚太極圖”.在如圖所示的陰陽魚圖案中,陰影部分可表示為
,太極圖無不躍居其上.這種廣為人知的太極圖,其形狀如陰陽兩魚互抱在一起,因而被稱為“陰陽魚太極圖”.在如圖所示的陰陽魚圖案中,陰影部分可表示為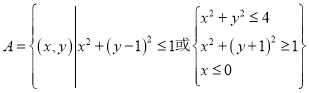 ,設點
,設點![]() ,則
,則![]() 的最大值與最小值之差是( )
的最大值與最小值之差是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解人們對于國家新頒布的“生育二胎放開”政策的熱度,現在某市進行調查,隨機調查了![]() 人,他們年齡的頻數分布及支持“生育二胎”人數如下表:
人,他們年齡的頻數分布及支持“生育二胎”人數如下表:
年齡 |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
支持“生二胎” |
|
|
|
|
|
|
(1)由以上統計數據填下面![]() 列聯表,并問是否有
列聯表,并問是否有![]() 的把握認為以
的把握認為以![]() 歲為分界點對“生育二胎放開”政策的支持度有差異;
歲為分界點對“生育二胎放開”政策的支持度有差異;
年齡不低于 | 年齡低于 | 合計 | |
支持 |
|
| |
不支持 |
|
| |
合計 |
(2)若對年齡在![]() 的被調查人中隨機選取兩人進行調查,恰好這兩人都支持“生育二胎放開”的概率是多少?
的被調查人中隨機選取兩人進行調查,恰好這兩人都支持“生育二胎放開”的概率是多少?
參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com