
 ,an2+(an+1+2)an+2an+1+1=0.
,an2+(an+1+2)an+2an+1+1=0.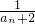 .
.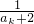 +2.
+2. 在t∈(1,2)內為增函數,
在t∈(1,2)內為增函數,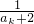 ∈(2,
∈(2, ),
), ,0),則-1<ak+1<0,
,0),則-1<ak+1<0, >a1=-
>a1=- 成立;
成立;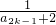 <a2k+2+
<a2k+2+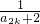 ,
,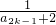 >-a2k-
>-a2k-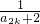 ,即a2k>a2k+1.
,即a2k>a2k+1.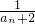 ,則an+2+an+1=-
,則an+2+an+1=-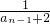 .
.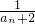 -
-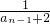 =
=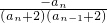 .
.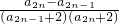 >0,
>0,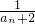 .當n=1時成立;②假設當n=k時結論成立,即-1<ak<0,那么當n=k+1時,ak+1=-(ak+2)-
.當n=1時成立;②假設當n=k時結論成立,即-1<ak<0,那么當n=k+1時,ak+1=-(ak+2)-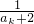 +2.由此導出-1<ak+1<0,當n=k+1時結論成立.由①②知,對一切n∈N*均有-1<an<0.
+2.由此導出-1<ak+1<0,當n=k+1時結論成立.由①②知,對一切n∈N*均有-1<an<0. >a1=-
>a1=- 成立;②假設當n=k(k≥1且k∈N)時結論成立,即a2k>a2k-1,由此能推導出a2k+2>a2k+1,當n=k+1時結論成立.由①②知對一切n∈N*均有a2n>a2n-1成立.
成立;②假設當n=k(k≥1且k∈N)時結論成立,即a2k>a2k-1,由此能推導出a2k+2>a2k+1,當n=k+1時結論成立.由①②知對一切n∈N*均有a2n>a2n-1成立.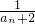 ,知an+2+an+1=-
,知an+2+an+1=-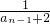 .由此能導出a2n+1-a2n-1=
.由此能導出a2n+1-a2n-1=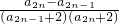 >0,即數列{a2n-1}為遞增數列.
>0,即數列{a2n-1}為遞增數列.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 3+4an |
| 12-4an |
| 1 | ||
an-
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com