Question

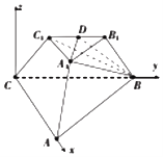
【題目】已知三棱臺ABC﹣A1B1C1中，平面BB1C1C⊥平面ABC，∠ACB=90°，BB1=CC1=B1C1=2，BC=4，AC=6
（1）求證：BC1⊥平面AA1C1C
（2）點D是B1C1的中點，求二面角A1﹣BD﹣B1的余弦值．

Answer 1

【答案】
（1）證明：梯形BB1C1C中，BB1=CC1=B1C1=2，BC=4得： ，從而BC1⊥CC1，

因為平面BB1C1C⊥平面ABC，且AC⊥BC，

所以AC⊥平面BB1C1C，因此BC1⊥AC，

因為AC∩CC1=C，所以BC1⊥平面AA1C1C

（2）解：如圖，以CA，CB所在直線分別為x軸，y軸，點C為原點建立空間直角坐標系，則A（6，0，0），B（0，4，0），C（0，0，0），C1（0，1， ），B1（0，3， ），D（0，2， ），A1（3，1， ），

平面BB1D的法向量 =（1，0，0），設平面AB1D的法向量為 =（x，y，z），

則 ，

令z= ，得 （ ， ），

所以所求二面角的余弦值是﹣ =﹣ ．

【解析】（1）證明BC1⊥CC1 ， BC1⊥AC，即可證明BC1⊥平面AA1C1C（2）以CA，CB所在直線分別為x軸，y軸，點C為原點建立空間直角坐標系，求出平面的法向量，即可求二面角A1﹣BD﹣B1的余弦值．
【考點精析】解答此題的關鍵在于理解直線與平面垂直的判定的相關知識，掌握一條直線與一個平面內的兩條相交直線都垂直，則該直線與此平面垂直；注意點：a)定理中的“兩條相交直線”這一條件不可忽視；b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想．