
(本小題滿分12分)已知函數(shù)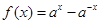 ,
,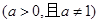 ,
,
(1) 判斷函數(shù) 的奇偶性,并證明;
的奇偶性,并證明;
(2) 判斷 的單調(diào)性,并說明理由。(不需要嚴格的定義證明,只要說出理由即可)
的單調(diào)性,并說明理由。(不需要嚴格的定義證明,只要說出理由即可)
(3) 若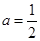 ,方程
,方程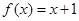 是否有根?如果有根
是否有根?如果有根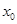 ,請求出一個長度為1的區(qū)間
,請求出一個長度為1的區(qū)間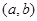 ,使
,使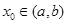 ;如果沒有,請說明理由。(注:區(qū)間
;如果沒有,請說明理由。(注:區(qū)間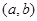 的長度=
的長度=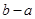 )
)
(1)  為奇函數(shù),證明:見解析;
為奇函數(shù),證明:見解析;
(2)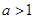 時,
時, 單調(diào)遞增;
單調(diào)遞增;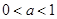 ,
, 單調(diào)遞減。
單調(diào)遞減。
(3)方程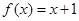 有根
有根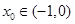 。
。
解析試題分析:(1)根據(jù)f(-x)=-f(x)可知此函數(shù)是奇函數(shù)。
(2) 分a>1和0<a<1兩種情況研究即可。a>1時,是兩個增函數(shù)的和,0<a<1時,是兩個減函數(shù)的和。
從而確定其單調(diào)性與底數(shù)a有關系。
(3) 當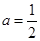 ,
,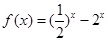 ,又
,又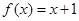 ,再令
,再令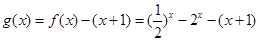 ,
,
然后判斷g(-1),g(0)的值,從而判斷y=g(x)在(-1,0)上是否存在零點,從而達到證明f(x)=x+1是否在(-1,0)上有根的目的。
(1)  為奇函數(shù)……………………1分
為奇函數(shù)……………………1分
證明:∵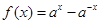 的定義域為R,關于原點對稱 …………………2分
的定義域為R,關于原點對稱 …………………2分
又 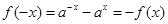 …………………………………………3分
…………………………………………3分
所以可知 為奇函數(shù)……………………………………………4分
為奇函數(shù)……………………………………………4分
(2) ∵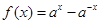 =
=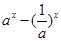
① 當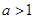 時,
時,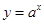 單調(diào)遞增,
單調(diào)遞增,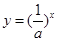 單調(diào)遞減,
單調(diào)遞減,
所以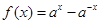 單調(diào)遞增…………………………………………………6分
單調(diào)遞增…………………………………………………6分
②當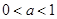 時,
時,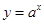 單調(diào)遞減,
單調(diào)遞減,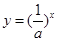 單調(diào)遞增,
單調(diào)遞增,
所以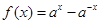 單調(diào)遞減。
單調(diào)遞減。
綜上可知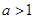 時,
時, 單調(diào)遞增;
單調(diào)遞增;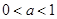 ,
, 單調(diào)遞減。
單調(diào)遞減。
………………………………………………8分
(3)當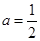 ,
,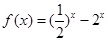 ,又
,又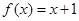
設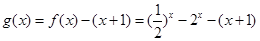 …………………………………9分
…………………………………9分
∵ 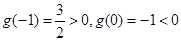 ………………………………………………10分
………………………………………………10分
∴ 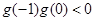 ,故
,故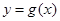 存在零點
存在零點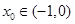
即方程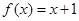 有根
有根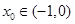 ……………………………………………12分
……………………………………………12分
考點:函數(shù)的單調(diào)性,奇偶性,函數(shù)的零點與方程的根的關系。
點評:掌握判斷函數(shù)奇偶性的方法:一要看定義域是否關于原點對稱,二要看f(-x)與f(x)的關系。
要掌握函數(shù)單調(diào)性的定義,它是證明抽象函數(shù)單調(diào)性的依據(jù)。函數(shù)的零點與方程的根的關系要搞清楚,它是實現(xiàn)根與零點的判斷轉(zhuǎn)化的依據(jù)。


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數(shù)學 來源: 題型:解答題
(本小題滿分12分)
已知函數(shù) 是奇函數(shù):
是奇函數(shù):
(1)求實數(shù)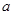 和
和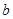 的值;
的值;
(2)證明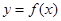 在區(qū)間
在區(qū)間 上的單調(diào)遞減
上的單調(diào)遞減
(3)已知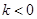 且不等式
且不等式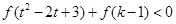 對任意的
對任意的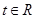 恒成立,求實數(shù)
恒成立,求實數(shù)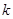 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
武漢市某地西瓜從2012年6月1日起開始上市。通過市場調(diào)查,得到西瓜種植成本Q(單位:元/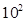 kg)與上市時間t(單位:天)的數(shù)據(jù)如下表:
kg)與上市時間t(單位:天)的數(shù)據(jù)如下表:
| 時間t | 50 | 110 | 250 |
| 種植成本Q | 150 | 108 | 150 |
 , Q= a
, Q= a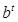 , Q=a
, Q=a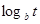 .
.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本題滿分12分)某公司試銷一種新產(chǎn)品,規(guī)定試銷時銷售單價不低于成本單價500元/件,又不高于800元/件,經(jīng)試銷調(diào)查,發(fā)現(xiàn)銷售量y(件)與銷售單價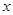 (元/件)之間,可近似看做一次函數(shù)
(元/件)之間,可近似看做一次函數(shù)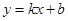 的關系(圖象如圖所示).
的關系(圖象如圖所示).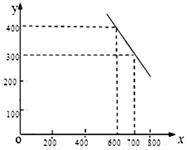
(1)根據(jù)圖象,求一次函數(shù)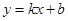 的表達式;
的表達式;
(2)設公司獲得的毛利潤(毛利潤=銷售總價-成本總價)為S元:
①求S關于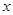 的函數(shù)表達式;
的函數(shù)表達式;
②求該公司可獲得的最大毛利潤,并求出此時相應的銷售單價.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com