
【題目】某校為了了解學生每天平均課外閱讀的時間(單位:分鐘),從本校隨機抽取了100名學生進行調查,根據收集的數據,得到學生每天課外閱讀時間的頻率分布直方圖,如圖所示,若每天課外閱讀時間不超過30分鐘的有45人.
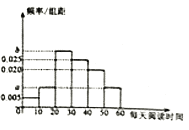
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)根據頻率分布直方圖,估計該校學生每天課外閱讀時間的中位數及平均值(同一組中的數據用該組區(qū)間的中點值代表).
 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:高中數學 來源: 題型:
【題目】已知符號函數sgnx= 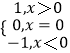 ,f(x)是R上的增函數,g(x)=f(x)﹣f(ax)(a>1),則( )
,f(x)是R上的增函數,g(x)=f(x)﹣f(ax)(a>1),則( )
A.sgn[g(x)]=sgnx
B.sgn[g(x)]=﹣sgnx
C.sgn[g(x)]=sgn[f(x)]
D.sgn[g(x)]=﹣sgn[f(x)]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業(yè)響應省政府號召,對現有設備進行改造,為了分析設備改造前后的效果,現從設備改造前后生產的大量產品中各抽取了![]() 件產品作為樣本,檢測一項質量指標值,若該項質量指標值落在
件產品作為樣本,檢測一項質量指標值,若該項質量指標值落在![]() 內的產品視為合格品,否則為不合格品.如圖是設備改造前的樣本的頻率分布直方圖,表
內的產品視為合格品,否則為不合格品.如圖是設備改造前的樣本的頻率分布直方圖,表![]() 是設備改造后的樣本的頻數分布表.
是設備改造后的樣本的頻數分布表.

表:設備改造后樣本的頻數分布表
質量指標值 |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
(1)完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為該企業(yè)生產的這種產品的質量指標值與設備改造有關;
的把握認為該企業(yè)生產的這種產品的質量指標值與設備改造有關;
設備改造前 | 設備改造后 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
(2)根據頻率分布直方圖和表 提供的數據,試從產品合格率的角度對改造前后設備的優(yōu)劣進行比較;
(3)企業(yè)將不合格品全部銷毀后,根據客戶需求對合格品進行登記細分,質量指標值落在![]() 內的定為一等品,每件售價
內的定為一等品,每件售價![]() 元;質量指標值落在
元;質量指標值落在![]() 或
或![]() 內的定為二等品,每件售價
內的定為二等品,每件售價![]() 元;其它的合格品定為三等品,每件售價
元;其它的合格品定為三等品,每件售價![]() 元.根據表
元.根據表![]() 的數據,用該組樣本中一等品、二等品、三等品各自在合格品中的頻率代替從所有產品中抽到一件相應等級產品的概率.現有一名顧客隨機購買兩件產品,設其支付的費用為
的數據,用該組樣本中一等品、二等品、三等品各自在合格品中的頻率代替從所有產品中抽到一件相應等級產品的概率.現有一名顧客隨機購買兩件產品,設其支付的費用為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望.
的分布列和數學期望.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個結論:
①從1,2,3,4,5中任取2個不同的數,事件![]() “取到的2個數之和為偶數”,事件
“取到的2個數之和為偶數”,事件![]() “取到的
“取到的
2個數均為偶數”,則![]() ;
;
②某班共有45名學生,其中30名男同學,15名女同學,老師隨機抽查了5名同學的作業(yè),用![]() 表示抽查到的女生的人數,則
表示抽查到的女生的人數,則![]() ;
;
③設隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,
,![]() ,則
,則![]() ;
;
④由直線![]() ,
,![]() ,曲線
,曲線![]() 及
及![]() 軸所圍成的圖形的面積是
軸所圍成的圖形的面積是![]() .
.
其中所有正確結論的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD外接于圓,AC是圓周角∠BAD的角平分線,過點C的切線與AD延長線交于點E,AC交BD于點F. 
(1)求證:BD∥CE;
(2)若AB是圓的直徑,AB=4,DE=1,求AD的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地合作農場的果園進入盛果期,果農利用互聯網電商渠道銷售蘋果,蘋果單果直徑不同則單價不同,為了更好的銷售,現從該合作農場果園的蘋果樹上隨機摘下了50個蘋果測量其直徑,經統(tǒng)計,其單果直徑分布在區(qū)間![]() 內(單位:
內(單位:![]() ),統(tǒng)計的莖葉圖如圖所示:
),統(tǒng)計的莖葉圖如圖所示:

(Ⅰ)按分層抽樣的方法從單果直徑落在![]() ,
,![]() 的蘋果中隨機抽取6個,則從
的蘋果中隨機抽取6個,則從![]() ,
,![]() 的蘋果中各抽取幾個?
的蘋果中各抽取幾個?
(Ⅱ)從(Ⅰ)中選出的6個蘋果中隨機抽取2個,求這兩個蘋果單果直徑均在![]() 內的概率;
內的概率;
(Ⅲ)以此莖葉圖中單果直徑出現的頻率代表概率,若該合作農場的果園有20萬個蘋果約5萬千克待出售,某電商提出兩種收購方案:方案![]() :所有蘋果均以5.5元/千克收購;方案
:所有蘋果均以5.5元/千克收購;方案![]() :按蘋果單果直徑大小分3類裝箱收購,每箱裝25個蘋果,定價收購方式為:單果直徑在
:按蘋果單果直徑大小分3類裝箱收購,每箱裝25個蘋果,定價收購方式為:單果直徑在![]() 內按35元/箱收購,在
內按35元/箱收購,在![]() 內按45元/箱收購,在
內按45元/箱收購,在![]() 內按55元/箱收購.包裝箱與分揀裝箱費用為5元/箱(該費用由合作農場承擔).請你通過計算為該合作農場推薦收益最好的方案.
內按55元/箱收購.包裝箱與分揀裝箱費用為5元/箱(該費用由合作農場承擔).請你通過計算為該合作農場推薦收益最好的方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系內,點![]() 實施變換
實施變換![]() 后,對應點為
后,對應點為![]() ,給出以下命題:
,給出以下命題:
①圓![]() 上任意一點實施變換
上任意一點實施變換![]() 后,對應點的軌跡仍是圓
后,對應點的軌跡仍是圓![]() ;
;
②若直線![]() 上每一點實施變換
上每一點實施變換![]() 后,對應點的軌跡方程仍是
后,對應點的軌跡方程仍是![]() 則
則![]() ;
;
③橢圓![]() 上每一點實施變換
上每一點實施變換![]() 后,對應點的軌跡仍是離心率不變的橢圓;
后,對應點的軌跡仍是離心率不變的橢圓;
④曲線![]() 上每一點實施變換
上每一點實施變換![]() 后,對應點的軌跡是曲線
后,對應點的軌跡是曲線![]() ,
,![]() 是曲線
是曲線![]() 上的任意一點,
上的任意一點,![]() 是曲線
是曲線![]() 上的任意一點,則
上的任意一點,則![]() 的最小值為
的最小值為![]() .
.
以上正確命題的序號是___________________(寫出全部正確命題的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() 是橢圓上一點.
是橢圓上一點.
(1)求橢圓的標準方程;
(2)過橢圓右焦點![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點,
兩點,![]() 是直線
是直線![]() 上任意一點.
上任意一點.
證明:直線![]() 的斜率成等差數列.
的斜率成等差數列.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com