
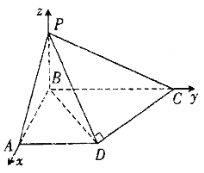
【題目】如圖,在四棱錐![]() 中,已知
中,已知![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,異面直線
,異面直線![]() 和
和![]() 所成角等于
所成角等于![]() .
.
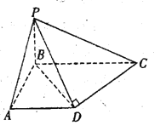
(1)求直線![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角的正切值為
所成銳二面角的正切值為![]() ?若存在,指出點
?若存在,指出點![]() 在棱
在棱![]() 上的位置;若不存在,說明理由.
上的位置;若不存在,說明理由.
【答案】(1)![]() ;(2)存在這樣的
;(2)存在這樣的![]() 點,
點,![]() 為棱
為棱![]() 上靠近
上靠近![]() 的三等分點.
的三等分點.
【解析】分析:(1)以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系.利用空間向量法能求出直線
軸,建立空間直角坐標系.利用空間向量法能求出直線![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(2)先假設棱![]() 上存在一點
上存在一點![]() ,求出平面
,求出平面![]() 與平面
與平面![]() 的法向量,進而求得二面角的余弦值,結合其正切值為
的法向量,進而求得二面角的余弦值,結合其正切值為![]() ,求出E點的位置.
,求出E點的位置.
詳解:解:(1)如圖,以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系.
軸,建立空間直角坐標系.
易知![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() .
.
設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
則![]() ,
,![]() ,
,
∵異面直線![]() 和
和![]() 所成角等于
所成角等于![]() ,
,
∴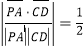 ,即
,即![]() ,解得
,解得![]() ,
,
∵![]() ,
,![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則由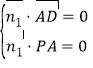 ,得
,得![]() ,所以可取
,所以可取![]() ,
,
∴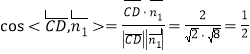 .
.
∴直線![]() 和平面
和平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
(2)假設存在,設![]() ,且
,且![]() ,則
,則![]() ,
,
![]() ,設平面
,設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則由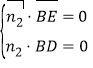 ,得
,得![]() ,
,
取![]() ,又有平面
,又有平面![]() 的法向量
的法向量![]() ,
,
由平面![]() 與平面
與平面![]() 所成銳二面角的正切值為
所成銳二面角的正切值為![]() ,可知余弦值為
,可知余弦值為![]() ,
,
由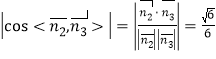 ,得
,得![]() ,
,
解得![]() 或
或![]() (不合題意).
(不合題意).
∴存在這樣的![]() 點,
點,![]() 為棱
為棱![]() 上靠近
上靠近![]() 的三等分點.
的三等分點.


科目:高中數學 來源: 題型:
【題目】定義:如果函數f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)滿足 ![]() ,
, ![]() 則稱函數f(x)是[a,b]上的“中值函數”.已知函數
則稱函數f(x)是[a,b]上的“中值函數”.已知函數 ![]() 是[0,m]上的“中值函數”,則實數m的取值范圍是( )
是[0,m]上的“中值函數”,則實數m的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點P在圓柱OO1的底面⊙O上,![]() 分別為⊙O、⊙O1的直徑,且
分別為⊙O、⊙O1的直徑,且![]() 平面
平面![]() .
.

(1)求證:![]() ;
;
(2)若圓柱![]() 的體積
的體積![]() ,
,
①求三棱錐A1﹣APB的體積.
②在線段AP上是否存在一點M,使異面直線OM與![]() 所成角的余弦值為
所成角的余弦值為![]() ?若存在,請指出M的位置,并證明;若不存在,請說明理由.
?若存在,請指出M的位置,并證明;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)估計該企業的職工對該部門評分不低于80的概率;
(3)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C1: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,P(﹣2,1)是C1上一點.
,P(﹣2,1)是C1上一點.
(1)求橢圓C1的方程;
(2)設A,B,Q是P分別關于兩坐標軸及坐標原點的對稱點,平行于AB的直線l交C1于異于P、Q的兩點C,D,點C關于原點的對稱點為E.證明:直線PD、PE與y軸圍成的三角形是等腰三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知過原點O的直線與函數![]() 的圖象交于A,B兩點,分別過A,B作y軸的平行線與函數
的圖象交于A,B兩點,分別過A,B作y軸的平行線與函數![]() 圖象交于C,D兩點,若
圖象交于C,D兩點,若![]() 軸,則四邊形ABCD的面積為_____.
軸,則四邊形ABCD的面積為_____.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱臺ABCD﹣A1B1C1D1中,AA1⊥底面ABCD,四邊形ABCD為菱形,∠BAD=120°,AB=AA1=2A1B1=2. (Ⅰ)若M為CD中點,求證:AM⊥平面AA1B1B;
(Ⅱ)求直線DD1與平面A1BD所成角的正弦值.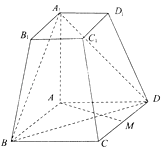
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓![]() 與
與![]() 軸的左右交點分別為
軸的左右交點分別為![]() ,與
,與![]() 軸正半軸的交點為
軸正半軸的交點為![]() .
.
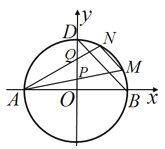
(1)若直線![]() 過點
過點![]() 并且與圓
并且與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若點![]() 是圓
是圓![]() 上第一象限內的點,直線
上第一象限內的點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是線段
是線段![]() 的中點,直線
的中點,直線![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com