
【題目】為了緩解日益擁堵的交通狀況,不少城市實施車牌競價策略,以控制車輛數量.某地車牌競價的基本規則是:①“盲拍”,即所有參與競拍的人都要網絡報價一次,每個人不知曉其他人的報價,也不知道參與當期競拍的總人數;②競價時間截止后,系統根據當期車牌配額,按照競拍人的出價從高到低分配名額.某人擬參加![]() 年
年![]() 月份的車牌競拍,他為了預測最低成交價,根據競拍網站的數據,統計了最近
月份的車牌競拍,他為了預測最低成交價,根據競拍網站的數據,統計了最近![]() 個月參與競拍的人數(見下表):
個月參與競拍的人數(見下表):
月份 |
|
|
|
|
|
月份編號 |
|
|
|
|
|
競拍人數 |
|
|
|
|
|
(1)由收集數據的散點圖發現,可用線性回歸模型擬合競拍人數![]() (萬人)與月份編號
(萬人)與月份編號![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程:
的線性回歸方程:![]() ,并預測
,并預測![]() 年
年![]() 月份參與競拍的人數.
月份參與競拍的人數.
(2)某市場調研機構從擬參加![]() 年
年![]() 月份車牌競拍人員中,隨機抽取了
月份車牌競拍人員中,隨機抽取了![]() 人,對他們的擬報價價格進行了調查,得到如下頻數分布表和頻率分布直方圖:
人,對他們的擬報價價格進行了調查,得到如下頻數分布表和頻率分布直方圖:
報價區間(萬元) |
|
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
|
(i)求![]() 、
、![]() 的值及這
的值及這![]() 位競拍人員中報價大于
位競拍人員中報價大于![]() 萬元的概率;
萬元的概率;
(ii)若![]() 年
年![]() 月份車牌配額數量為
月份車牌配額數量為![]() ,假設競拍報價在各區間分布是均勻的,請你根據以上抽樣的數據信息,預測(需說明理由)競拍的最低成交價.
,假設競拍報價在各區間分布是均勻的,請你根據以上抽樣的數據信息,預測(需說明理由)競拍的最低成交價.
參考公式及數據:①回歸方程![]() ,其中
,其中 ,
,![]() ;
;
②![]() ,
,![]() .
.

【答案】(1)2018年5月份參與競拍的人數估計為2萬人;(2)①![]()
概率為![]() ②最低成交價為
②最低成交價為![]() 萬元..
萬元..
【解析】分析:(1)先求均值![]() ,
,![]() ,代入公式得
,代入公式得![]() ,再根據
,再根據![]() 得
得![]() ,最后根據線性回歸方程求預估值,(2) ①根據頻數等于總數與頻率的乘積得a,根據頻率分布直方圖中所有小長方體面積和為1求b,再根據頻率等于頻數除以總數得結果;②先求報價在最低成交價以上人數占總人數比例,再對應頻率分布直方圖頻率,確定結果.
,最后根據線性回歸方程求預估值,(2) ①根據頻數等于總數與頻率的乘積得a,根據頻率分布直方圖中所有小長方體面積和為1求b,再根據頻率等于頻數除以總數得結果;②先求報價在最低成交價以上人數占總人數比例,再對應頻率分布直方圖頻率,確定結果.
詳解:(1)易知![]() ,
,![]() ,
,
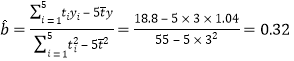 ,
,
![]() ,
,
則![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,
,
當![]() 時,
時,![]() ,即2018年5月份參與競拍的人數估計為2萬人.
,即2018年5月份參與競拍的人數估計為2萬人.
(2)(i)由![]() 解得
解得![]() ;
;
由頻率和為1,得![]() ,解得
,解得![]() ,
,
![]() 位競拍人員報價大于5萬元得人數為
位競拍人員報價大于5萬元得人數為![]() 人;
人;
這![]() 位競拍人員中報價大于
位競拍人員中報價大于![]() 萬元的概率為
萬元的概率為![]()
(ii)2018年5月份實際發放車牌數量為3000,根據競價規則,報價在最低成交價以上人數占總人數比例為![]() ;又由頻率分布直方圖知競拍報價大于6萬元的頻率為
;又由頻率分布直方圖知競拍報價大于6萬元的頻率為![]() ;
;
所以,根據統計思想(樣本估計總體)可預測2018年5月份競拍的最低成交價為![]() 萬元.
萬元.


 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】下列各題中,哪些p是q的充要條件?
(1)p:四邊形是正方形,q:四邊形的對角線互相垂直且平分;
(2)p:兩個三角形相似,q:兩個三角形三邊成比例;
(3)![]() ,
,![]() ,
,![]() ;
;
(4)![]() 是一元二次方程
是一元二次方程![]() 的一個根,
的一個根,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)求函數![]() 的最大值和最小值,并求取得最大值和最小值時對應的
的最大值和最小值,并求取得最大值和最小值時對應的![]() 的值;
的值;
(2)設方程![]() 在區間
在區間![]() 內有兩個相異的實數根
內有兩個相異的實數根![]() 求
求![]() 的值;
的值;
(3)如果對于區間![]() 上的任意一個
上的任意一個![]() 都有
都有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國2019年新年賀歲大片《流浪地球》自上映以來引發了社會的廣泛關注,受到了觀眾的普遍好評.假設男性觀眾認為《流浪地球》好看的概率為![]() ,女性觀眾認為《流浪地球》好看的概率為
,女性觀眾認為《流浪地球》好看的概率為![]() .某機構就《流浪地球》是否好看的問題隨機采訪了4名觀眾(其中2男2女).
.某機構就《流浪地球》是否好看的問題隨機采訪了4名觀眾(其中2男2女).
(1)求這4名觀眾中女性認為好看的人數比男性認為好看的人數多的概率;
(2)設![]() 表示這4名觀眾中認為《流浪地球》好看的人數,求
表示這4名觀眾中認為《流浪地球》好看的人數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|f(x)=lg(x﹣1)![]() },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a![]() ,求A∪B;
,求A∪B;
(2)若A∩B=![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在古代三國時期吳國的數學家趙爽創制了一幅“趙爽弦圖”,由四個全等的直角三角形圍成一個大正方形,中間空出一個小正方形(如圖陰影部分)。若直角三角形中較小的銳角為a。現向大正方形區城內隨機投擲一枚飛鏢,要使飛鏢落在小正方形內的概率為![]() ,則
,則![]() _____________。
_____________。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業產值在2008年~2017年的年增量(即當年產值比前一年產值增加的量)統計圖如圖所示(單位:萬元),下列說法正確的是( )
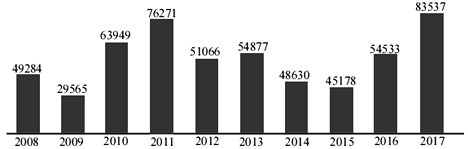
A. 2009年產值比2008年產值少
B. 從2011年到2015年,產值年增量逐年減少
C. 產值年增量的增量最大的是2017年
D. 2016年的產值年增長率可能比2012年的產值年增長率低
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com