Question

【題目】已知函數(shù).

（1）討論函數(shù)的單調(diào)性；

（2）若，函數(shù)在區(qū)間上恰有兩個(gè)零點(diǎn)，求的取值范圍.

Answer 1

【答案】（1）詳見解析；（2）.

【解析】

（1）求出，對(duì)的正負(fù)分類討論即可。

（2）利用（1）中的結(jié)論即可判斷在上單調(diào)遞減，在上單調(diào)遞增，對(duì)與區(qū)間的關(guān)系分類討論即可判斷在的單調(diào)性，從而根據(jù)零點(diǎn)個(gè)數(shù)列不等式組即可求解。

解：（1）的定義域?yàn)?/span>，

.

①時(shí)，，所以在上單調(diào)遞增；

②時(shí)，由得，得.

即在上單調(diào)遞減，在上單調(diào)遞增.

綜上：當(dāng)時(shí)，在上單調(diào)遞減；

當(dāng)時(shí)，在上單調(diào)遞減，在上單調(diào)遞增.

（2）當(dāng)時(shí)，由（1）知在上單調(diào)遞減，在上單調(diào)遞增，

①若，即時(shí)，在上單調(diào)遞增，

，在區(qū)間上無零點(diǎn).

②若，即時(shí)，在上單調(diào)遞減，在上單調(diào)遞增，

.

∵在區(qū)間上恰有兩個(gè)零點(diǎn)，

∴，∴.

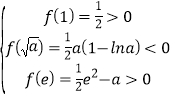③若，即時(shí)，在上單調(diào)遞減，

，，在區(qū)間上有一個(gè)零點(diǎn).

綜上，在區(qū)間上恰有兩個(gè)零點(diǎn)時(shí)的取值范圍是.