
(12分)已知函數 (
( 是不為零的實數,
是不為零的實數, 為自然對數的底數).
為自然對數的底數).
(1)若曲線 與
與 有公共點,且在它們的某一公共點處有共同的切線,求
有公共點,且在它們的某一公共點處有共同的切線,求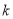 的值;
的值;
(2)若函數 在區間
在區間 內單調遞減,求此時
內單調遞減,求此時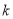 的取值范圍.
的取值范圍.
(1) (2)當
(2)當 時,函數
時,函數 在區間
在區間 內單調遞減.
內單調遞減.
【解析】
試題分析:(1)利用導數的幾何意義求曲線在某點處的切線方程,注意這個點的切點的位置. (2)第二問關鍵是利用函數的單調性與導數的關系把所求問題轉化為求函數的其它問題.(3)若可導函數 在指定的區間
在指定的區間 上單調遞增(減),求參數問題,可轉化為
上單調遞增(減),求參數問題,可轉化為
 恒成立,從而構建不等式,要注意“=”是否可以取到.
恒成立,從而構建不等式,要注意“=”是否可以取到.
試題解析:(1)設曲線 與
與 有共同切線的公共點為
有共同切線的公共點為 ,則
,則 .
.
又曲線 與
與 在點
在點 處有共同切線,且
處有共同切線,且 ,
, ,
,
∴ ,
,
解得  .
.
(2)由 得函數
得函數 ,
,
所以

 .
.
又由區間 知,
知, ,解得
,解得 ,或
,或 .
.
①當 時,由
時,由
 ,得
,得 ,即函數
,即函數 的單調減區間為
的單調減區間為 ,要使得函數
,要使得函數 在區間
在區間 內單調遞減,則有
內單調遞減,則有
解得
②當 時,由
時,由
 ,得
,得 ,或
,或 ,即函數
,即函數 的單調減區間為
的單調減區間為 和
和 ,
,
要使得函數 在區間
在區間 內單調遞減,則有
內單調遞減,則有
 ,或
,或 ,
,
這兩個不等式組均無解.
綜上,當 時,函數
時,函數 在區間
在區間 內單調遞減.
內單調遞減.
考點:(1)求切線方程;(2)根據函數的單調性求參量的問題.


科目:高中數學 來源:2015屆浙江省等四校高三上學期期中聯考理科數學試卷(解析版) 題型:選擇題
已知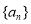 是等比數列,其中
是等比數列,其中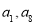 是關于
是關于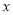 的方程
的方程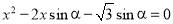 的兩根,且
的兩根,且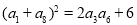 ,則銳角
,則銳角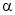 的值為( )
的值為( )
A.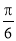 B.
B.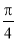 C.
C.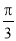 D.
D.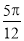
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省新高考單科綜合調研卷理科數學試卷一(解析版) 題型:選擇題
若將函數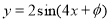 的圖象向右平移
的圖象向右平移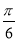 個單位,得到的圖象關于y軸對稱,則
個單位,得到的圖象關于y軸對稱,則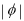 的最小值是 ( )
的最小值是 ( )
A.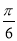 B.
B.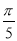 C.
C.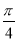 D.
D.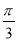
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省富陽市高二下學期期中考試理科數學試卷(解析版) 題型:填空題
設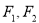 為橢圓
為橢圓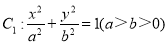 與雙曲線
與雙曲線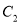 的公共左右焦點,它們在第一象限內交于點
的公共左右焦點,它們在第一象限內交于點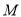 ,△
,△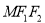 是以線段
是以線段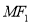 為底邊的等腰三角形,且
為底邊的等腰三角形,且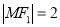 .若橢圓
.若橢圓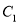 的離心率
的離心率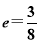 ,則雙曲線
,則雙曲線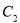 的離心率是__________.
的離心率是__________.
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省富陽市高二下學期期中考試理科數學試卷(解析版) 題型:選擇題
函數 的定義域為
的定義域為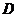 ,若存在閉區間
,若存在閉區間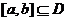 ,使得函數
,使得函數 滿足:①
滿足:① 在
在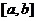 內是單調函數;②
內是單調函數;② 在
在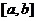 上的值域為
上的值域為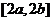 ,則稱區間
,則稱區間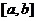 為
為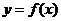 的“倍值區間”.下列函數中存在“倍值區間”的有( )
的“倍值區間”.下列函數中存在“倍值區間”的有( )
① ;
;
② ;
;
③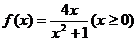 ;
;
④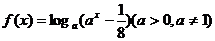
A.①②③④ B.①②④ C.①③④ D.①③
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省嘉興市高三新高考調研二文科數學試卷(解析版) 題型:填空題
定義在R上運算 :x
:x y=
y=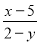 ,若關于x的不等式x
,若關于x的不等式x (x+3-a)>0的解集為A,B=[-3,3],若
(x+3-a)>0的解集為A,B=[-3,3],若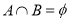 ,則
,則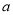 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com