
【題目】設雙曲線![]() 的方程為
的方程為![]() .
.
(1)設![]() 是經過點
是經過點![]() 的直線,且和
的直線,且和![]() 有且僅有一個公共點,求
有且僅有一個公共點,求![]() 的方程;
的方程;
(2)設![]() 是
是![]() 的一條漸近線,
的一條漸近線,![]() 、
、![]() 是
是![]() 上相異的兩點.若點
上相異的兩點.若點![]() 是
是![]() 上的一點,
上的一點,![]() 關于點
關于點![]() 的對稱點記為
的對稱點記為![]() ,
,![]() 關于點
關于點![]() 的對稱點記為
的對稱點記為![]() .試判斷點
.試判斷點![]() 是否可能在
是否可能在![]() 上,并說明理由.
上,并說明理由.
【答案】(1)![]() 或
或![]() 或
或![]() 或
或![]() ;(2)點
;(2)點![]() 不可能在雙曲線
不可能在雙曲線![]() 上,理由詳見解析.
上,理由詳見解析.
【解析】
(1)對所求直線分三種情況討論:①![]() 軸,驗證即可;②直線
軸,驗證即可;②直線![]() 與雙曲線相切,設出直線方程,與雙曲線的方程聯立,由
與雙曲線相切,設出直線方程,與雙曲線的方程聯立,由![]() 求出直線的斜率,可得出直線
求出直線的斜率,可得出直線![]() 的方程;③直線
的方程;③直線![]() 與雙曲線的漸近線平行,可得出直線
與雙曲線的漸近線平行,可得出直線![]() 的方程.綜合可得出所求直線
的方程.綜合可得出所求直線![]() 的方程;
的方程;
(2)假設點![]() 在雙曲線
在雙曲線![]() 上,設直線
上,設直線![]() 的方程為
的方程為![]() ,設點
,設點![]() 、
、![]() ,
,![]() ,求出點
,求出點![]() 、
、![]() 的坐標,再將點
的坐標,再將點![]() 的坐標代入雙曲線
的坐標代入雙曲線![]() 的方程驗證即可得出結論.
的方程驗證即可得出結論.
(1)①當直線![]() 的斜率不存在時,方程為
的斜率不存在時,方程為![]() ,顯然與雙曲線
,顯然與雙曲線![]() 相切,只有一個交點,符合題意,
相切,只有一個交點,符合題意,
②當直線![]() 的斜率存在且與雙曲線
的斜率存在且與雙曲線![]() 相切時,設斜率為
相切時,設斜率為![]() ,
,
則直線![]() 的方程為
的方程為![]() ,即
,即![]() ,
,
聯立方程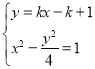 ,消去
,消去![]() 得
得![]() ,
,
![]() 直線
直線![]() 和雙曲線
和雙曲線![]() 有且僅有一個公共點,
有且僅有一個公共點,![]() ,
,
化簡得![]() ,解得
,解得![]() ,此時,直線
,此時,直線![]() 的方程為
的方程為![]() ,即
,即![]() ;
;
③當直線![]() 與雙曲線
與雙曲線![]() 的漸近線平行時,也與雙曲線
的漸近線平行時,也與雙曲線![]() 有且僅有一個公共點,
有且僅有一個公共點,
![]() 雙曲線
雙曲線![]() 的漸近線方程為
的漸近線方程為![]() ,
,![]() 直線
直線![]() 的斜率為
的斜率為![]() ,
,
所以,直線![]() 的方程為
的方程為![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
綜上所述,直線![]() 的方程為
的方程為![]() 或
或![]() 或
或![]() 或
或![]() ;
;
(2)假設點![]() 在雙曲線
在雙曲線![]() 上,
上,
不妨設直線![]() 方程為
方程為![]() ,設點
,設點![]() 、
、![]() 、
、![]() ,
,
![]() 關于點
關于點![]() 的對稱點記為
的對稱點記為![]() ,
,![]() 點
點![]() ,
,
![]() 關于點
關于點![]() 的對稱點記為
的對稱點記為![]() ,
,![]() 點
點![]() ,
,
![]() 點
點![]() 在雙曲線
在雙曲線![]() 上,
上,![]() ,
,
![]() ,
,
∴![]() ,
,
又![]() 點
點![]() 在雙曲線
在雙曲線![]() 上,
上,![]() ,
,
上式化為![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
![]() ,則
,則![]() ,此式顯然不成立,
,此式顯然不成立,
故假設不成立,所以點![]() 不可能在雙曲線
不可能在雙曲線![]() 上.
上.


 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的左頂點
的左頂點![]() ,且點
,且點![]() 在橢圓上,
在橢圓上, ![]() 分別是橢圓的左、右焦點。過點
分別是橢圓的左、右焦點。過點![]() 作斜率為
作斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于另一點
于另一點![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于點
于點![]() .
.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為等腰三角形,求點
為等腰三角形,求點![]() 的坐標;
的坐標;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】時值金秋十月,正是秋高氣爽,陽光明媚的美好時刻。復興中學一年一度的校運會正在密鑼緊鼓地籌備中,同學們也在熱切地期盼著,都想為校運會出一份力。小智同學則通過對學校有關部門的走訪,隨機地統計了過去許多年中的五個年份的校運會“參與”人數及相關數據,并進行分析,希望能為運動會組織者科學地安排提供參考。
附:①過去許多年來學校的學生數基本上穩定在3500人左右;②“參與”人數是指運動員和志愿者,其余同學均為“啦啦隊員”,不計入其中;③用數字1、2、3、4、5表示小智同學統計的五個年份的年份數,今年的年份數是6;
統計表(一)
年份數x | 1 | 2 | 3 | 4 | 5 |
“參與”人數(y千人) | 1.9 | 2.3 | 2.0 | 2.5 | 2.8 |
統計表(二)
高一(3)(4)班參加羽毛球比賽的情況:
男生 | 女生 | 小計 | |
參加(人數) | 26 | b | 50 |
不參加(人數) | c | 20 | |
小計 | 44 | 100 |
(1)請你與小智同學一起根據統計表(一)所給的數據,求出“參與”人數y關于年份數x的線性回歸方程![]() ,并預估今年的校運會的“參與”人數;
,并預估今年的校運會的“參與”人數;
(2)學校命名“參與”人數占總人數的百分之八十及以上的年份為“體育活躍年”.如果該校每屆校運會的“參與”人數是互不影響的,且假定小智同學對今年校運會的“參與”人數的預估是正確的,并以這6個年份中的“體育活躍年”所占的比例作為任意一年是“體育活躍年”的概率。現從過去許多年中隨機抽取9年來研究,記這9年中“體活躍年”的個數為隨機變量![]() ,試求隨機變量
,試求隨機變量的分布列、期望
![]() 和方差
和方差![]() ;
;
(3)根據統計表(二),請問:你能否有超過60%的把握認為“羽毛球運動”與“性別”有關?
參考公式和數據一: ,
,![]() ,
,![]() ,
,![]()
參考公式二: ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】阿波羅尼斯(約公元前![]() 年)證明過這樣一個命題:平面內到兩定點距離之比為常數
年)證明過這樣一個命題:平面內到兩定點距離之比為常數![]() 的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.若平面內兩定點
的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.若平面內兩定點![]() 、
、![]() 間的距離為
間的距離為![]() ,動點
,動點![]() 滿足
滿足![]() ,則
,則![]() 的最小值為( )
的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市食品藥品監督管理局開展2019年春季校園餐飲安全檢查,對本市的8所中學食堂進行了原料采購加工標準和衛生標準的檢查和評分,其評分情況如下表所示:
中學編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采購加工標準評分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
衛生標準評分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x與y之間具有線性相關關系,求y關于x的線性回歸方程;(精確到0.1)
(2)現從8個被檢查的中學食堂中任意抽取兩個組成一組,若兩個中學食堂的原料采購加工標準和衛生標準的評分均超過80分,則組成“對比標兵食堂”,求該組被評為“對比標兵食堂”的概率.
參考公式: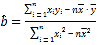 ,
,![]() ;
;
參考數據:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】食品安全問題越來越引起人們的重視,農藥、化肥的濫用對人民群眾的健康帶來一定的危害,為了給消費者帶來放心的蔬菜,某農村合作社每年投入200萬元,搭建了甲、乙兩個無公害蔬菜大棚,每個大棚至少要投入20萬元,其中甲大棚種西紅柿,乙大棚種黃瓜,根據以往的種菜經驗,發現種西紅柿的年收入![]() 種黃瓜的年收入
種黃瓜的年收入![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() .設甲大棚的投入為
.設甲大棚的投入為![]() (單位:萬元),每年兩個大棚的總收益為
(單位:萬元),每年兩個大棚的總收益為![]() (單位:萬元)
(單位:萬元)
(1)求![]() 的值;
的值;
(2)試問如何安排甲、乙兩個大棚的投入,才能使總收益![]() 最大?
最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com