
【題目】已知函數![]() ,其中e為自然對數的底數.
,其中e為自然對數的底數.
(1)若函數![]() 的極小值為
的極小值為![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,證明:當
,證明:當![]() 時,
時,![]() 成立.
成立.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】
(1)求出函數的導數,分![]() 和
和![]() 兩種情況討論,當
兩種情況討論,當![]() 時可得到
時可得到![]() ,令
,令![]() ,根據函數的單調性求出a的值即可;
,根據函數的單調性求出a的值即可;
(2)要證原不等式即證![]() ,然后利用導數分別證明不等式
,然后利用導數分別證明不等式![]() 和
和![]() 即可.
即可.
(1)函數![]() 的定義域是R,
的定義域是R,![]()
![]() 時,
時,![]() 對
對![]() 恒成立,
恒成立,
∴![]() 在R上單調遞減,函數無極值,
在R上單調遞減,函數無極值,
![]() 時,令
時,令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴![]() 時,
時,![]() 取極小值-1,
取極小值-1,
∴![]() ,即
,即![]() ,
,
令![]() ,
,
則![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
∵![]() ,∴
,∴![]() ;
;
(2)∵![]() ,∴
,∴![]()
∴![]() ,
,
令![]()
∴![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴![]() 時,
時,![]() 取得極小值,
取得極小值,
又∵![]() ,
,![]() ,
,
∴存在![]() 使得
使得![]() ,
,
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∵![]() ,∴
,∴![]() ,
,
∴![]() 時,
時,![]() ,即
,即![]() ,
,
令![]() ,
,
則![]() 對于
對于![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() ,即當
,即當![]() 時,
時,![]() ,
,
∴![]() 時,
時,![]() ,
,
∴![]()
故![]() 時,
時,![]() 成立.
成立.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】學校藝術節對![]() 四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”; 乙說:“
作品獲得一等獎”; 乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() 兩件作品未獲得一等獎”; 丁說:“是
兩件作品未獲得一等獎”; 丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
評獎揭曉后,發現這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某部門在上班高峰時段對甲、乙兩座地鐵站各隨機抽取了50名乘客,統計其乘車等待時間(指乘客從進站口到乘上車的時間,單位:分鐘)將統計數據按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分組,制成頻率分布直方圖如圖所示:
分組,制成頻率分布直方圖如圖所示:
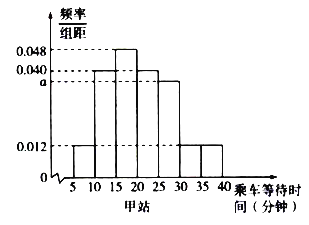
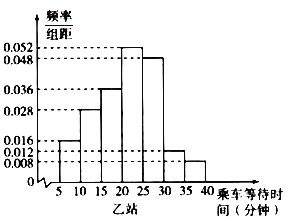
(1)求a的值;
(2)記A表示事件“在上班高峰時段某乘客在甲站乘車等待時間少于20分鐘”試估計A的概率;
(3)假設同組中的每個數據用該組區間左端點值來估計,記在上班高峰時段甲、乙兩站各抽取的50名乘客乘車的平均等待時間分別為![]() ,求
,求![]() 的值,并直接寫出
的值,并直接寫出![]() 與
與![]() 的大小關系.
的大小關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著現代電子技術的迅猛發展,關于元件和系統可靠性的研究已發展成為一門新的學科——可靠性理論.在可靠性理論中,一個元件正常工作的概率稱為該元件的可靠性.元件組成系統,系統正常工作的概率稱為該系統的可靠性.現有![]() (
(![]() ,
,![]() )種電子元件,每種2個,每個元件的可靠性均為
)種電子元件,每種2個,每個元件的可靠性均為![]() (
(![]() ).當某元件不能正常工作時,該元件在電路中將形成斷路.現要用這
).當某元件不能正常工作時,該元件在電路中將形成斷路.現要用這![]() 個元件組成一個電路系統,有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態時,系統正常工作.
個元件組成一個電路系統,有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態時,系統正常工作.
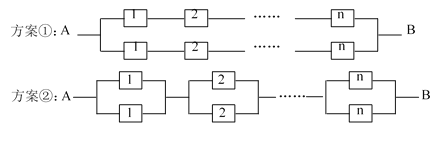
(1)(i)分別寫出按方案①和方案②建立的電路系統的可靠性![]() 、
、![]() (用
(用![]() 和
和![]() 表示);
表示);
(ii)比較![]() 與
與![]() 的大小,說明哪種連接方案更穩定可靠;
的大小,說明哪種連接方案更穩定可靠;
(2)設![]() ,
,![]() ,已知按方案②建立的電路系統可以正常工作,記此時系統中損壞的元件個數為
,已知按方案②建立的電路系統可以正常工作,記此時系統中損壞的元件個數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com