
【題目】海關對同時從![]() 三個不同地區進口的某種商品進行抽樣檢測,從各地區進口此種商品的數量(單位:件)如表所示,工作人員用分層抽樣的方法從這些商品中共抽取7件樣品進行檢測.
三個不同地區進口的某種商品進行抽樣檢測,從各地區進口此種商品的數量(單位:件)如表所示,工作人員用分層抽樣的方法從這些商品中共抽取7件樣品進行檢測.
地區 |
|
|
|
數量 | 200 | 50 | 100 |
(1)求這7件樣品中來自![]() 各地區樣品的數量;
各地區樣品的數量;
(2)若在這7件樣品中隨機抽取2件送往甲機構進行進一步檢測,求這2件商品來自相同地區的概率.
【答案】(1)4,1,2;(2)![]() .
.
【解析】
(1)先計算出抽樣比,進而可求出這7件樣品來自![]() ,
,![]() ,
,![]() 各地區商品的數量;
各地區商品的數量;
(2)先計算在這7件樣品中隨機抽取2件的基本事件總數,及這2件商品來自相同地區的事件個數,代入古典概型概率計算公式,可得答案;
解:(1)∵樣本容量與總體中的個數的比為![]()
∴樣本中包含三個地區的個體數量分別為:
![]() ,
,![]() ,
,![]()
∴![]() 三個地區的商品被選取的件數分別為4,1,2.
三個地區的商品被選取的件數分別為4,1,2.
(2)設7件來自![]() 三個地區的樣品分別為:
三個地區的樣品分別為:![]()
解從7件樣品中抽取的這2件商品構成的所有基本事件為:
![]()
![]()
![]() ,共21個.
,共21個.
每個樣品被抽到的機會均等,因此這些基本事件的出現是等可能的.
記事件![]() :“抽取的這2件商品來自相同地區,”,則事件
:“抽取的這2件商品來自相同地區,”,則事件![]() 包含的基本事件有:
包含的基本事件有:
![]() 共7個.
共7個.
所以![]() ,即這2件商品來自相同地區的概率為
,即這2件商品來自相同地區的概率為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且過點
的焦點重合,且過點![]() .過點
.過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓的左頂點.
為橢圓的左頂點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市公交公司為了鼓勵廣大市民綠色出行,計劃在某個地段增設一個起點站,為了研究車輛發車的間隔時間![]() 與乘客等候人數
與乘客等候人數![]() 之間的關系,經過抽樣調查五個不同時段的情形,統計得到如下數據:
之間的關系,經過抽樣調查五個不同時段的情形,統計得到如下數據:
間隔時間( | 8 | 10 | 12 | 14 | 16 |
等候人數( | 16 | 19 | 23 | 26 | 29 |
調查小組先從這5組數據中選取其中的4組數據求得線性回歸方程,再用剩下的1組數據進行檢驗,檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數![]() ,再求
,再求![]() 與實際等候人數
與實際等候人數![]() 的差,若差值的絕對值不超過1,則稱所求的回歸方程是“理想回歸方程”.
的差,若差值的絕對值不超過1,則稱所求的回歸方程是“理想回歸方程”.
(1)若選取的是前4組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并判斷所求方程是否是“理想回歸方程”;
,并判斷所求方程是否是“理想回歸方程”;
(2)為了使等候的乘客不超過38人,試用所求方程估計間隔時間最多可以設為多少分鐘?
參考公式:用最小二乘法求線性回歸方程![]() 的系數公式:
的系數公式:
 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)設![]() ,求證:數列{bn}是等差數列,并求出{an}的通項公式.
,求證:數列{bn}是等差數列,并求出{an}的通項公式.
(2)設![]() ,數列{cncn+2}的前n項和為Tn,是否存在正整數m,使得
,數列{cncn+2}的前n項和為Tn,是否存在正整數m,使得![]() 對于n∈N*,恒成立?若存在,求出m的最小值;若不存在,請說明.
對于n∈N*,恒成立?若存在,求出m的最小值;若不存在,請說明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高二期中考試后,教務處計劃對全年級數學成績進行統計分析,從男、女生中各隨機抽取100名學生,分別制成了男生和女生數學成績的頻率分布直方圖,如圖所示.

(1)若所得分數大于等于80分認定為優秀,求男、女生優秀人數各有多少人?
(2)在(1)中的優秀學生中用分層抽樣的方法抽取5人,從這5人中任意任取2人,求至少有1名男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中,直線
軸的正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(Ⅰ)寫出直線![]() 與曲線
與曲線![]() 的直角坐標方程:
的直角坐標方程:
(Ⅱ)過點![]() 平行于直線
平行于直線![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 軌跡的直角坐標方程.
軌跡的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學團委組織了“紀念抗日戰爭勝利73周年”的知識競賽,從參加競賽的學生中抽出60名學生,將其成績(均為整數)分成六段![]() ,
,![]() ,…,
,…,![]() 后,畫出如圖所示的部分頻率分布直方圖.觀察圖形給出的信息,回答下列問題:
后,畫出如圖所示的部分頻率分布直方圖.觀察圖形給出的信息,回答下列問題:
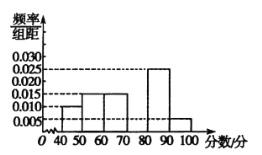
(1)求第四組的頻率,并補全這個頻率分布直方圖;
(2)估計這次競賽的及格率(60分及以上為及格)和平均分(同一組中的數據用該組區間的中點值代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的偶函數,且當
上的偶函數,且當![]() 時,
時, ![]() .現已畫出函數
.現已畫出函數![]() 在
在![]() 軸左側的圖象,如圖所示,并根據圖象:
軸左側的圖象,如圖所示,并根據圖象:

(1)直接寫出函數![]() ,
, ![]() 的增區間;
的增區間;
(2)寫出函數![]() ,
, ![]() 的解析式;
的解析式;
(3)若函數![]() ,
, ![]() ,求函數
,求函數![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com