
【題目】在貫徹中共中央、國務院關(guān)于精準扶貧政策的過程中,某單位在某市定點幫扶某村100戶貧困戶.為了做到精準幫扶,工作組對這100戶村民的年收入情況、危舊房情況、患病情況等進行調(diào)查,并把調(diào)查結(jié)果轉(zhuǎn)化為各戶的貧困指標,將指標![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五組,得到如圖所示的頻率分布直方圖.規(guī)定若
分成五組,得到如圖所示的頻率分布直方圖.規(guī)定若![]() ,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”;當
,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”;當![]() 時,認定該戶為“亟待幫住戶”.
時,認定該戶為“亟待幫住戶”.
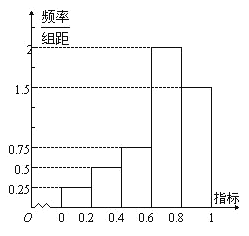
(1)為了更好的了解和幫助該村的這些貧困戶,決定用分層抽樣的方法從這100戶中隨機抽取20戶進行更深入的調(diào)查,求應該抽取“絕對貧困戶”的戶數(shù);
(2)從這20戶中任取3戶,求“絕對貧困戶”多于“相對貧困戶”的概率;
(3)現(xiàn)在從(1)中所抽取的“絕對貧困戶”中任取3戶,用![]() 表示所選3戶中“亟待幫助戶”的戶數(shù),求
表示所選3戶中“亟待幫助戶”的戶數(shù),求![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望![]() .
.
【答案】(1)6戶,(2)![]() ,(3)分布列見解析,
,(3)分布列見解析,![]() .
.
【解析】
(1)根據(jù)頻數(shù)=樣本容量×頻率,可得結(jié)果;
(2)根據(jù)古典概型的概率公式可得結(jié)果;
(3)![]() 的所有可能的取值為0,1,2,3,根據(jù)古典概型概率公式求出
的所有可能的取值為0,1,2,3,根據(jù)古典概型概率公式求出![]() 的各個取值的概率可得分布列,根據(jù)數(shù)學期望公式可得數(shù)學期望的值.
的各個取值的概率可得分布列,根據(jù)數(shù)學期望公式可得數(shù)學期望的值.
(1)由直方圖可知,“絕對貧困戶”的頻率為![]() ,
,
所以應該抽取“絕對貧困戶”的戶數(shù)為![]() 戶.
戶.
(2)這20戶中,“絕對貧困戶”的戶數(shù)為6戶,“相對貧困戶”的戶數(shù)為14戶,
所以“絕對貧困戶”多于“相對貧困戶”的概率為![]()
![]() .
.
(3)從(1)中所抽取的“絕對貧困戶”中,“亟待幫助戶”的戶數(shù)為3戶,
所以![]() 的所有可能的取值為0,1,2,3.
的所有可能的取值為0,1,2,3.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]()
![]()
![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】盲盒里面通常裝的是動漫、影視作品的周邊,或者設計師單獨設計出來的玩偶.由于盒子上沒有標注,購買者只有打開才會知道自己買到了什么,因此這種驚喜吸引了眾多年輕人,形成了“盲盒經(jīng)濟”.某款盲盒內(nèi)可能裝有某一套玩偶的![]() 、
、![]() 、
、![]() 三種樣式,且每個盲盒只裝一個.
三種樣式,且每個盲盒只裝一個.
(1)若每個盲盒裝有![]() 、
、![]() 、
、![]() 三種樣式玩偶的概率相同.某同學已經(jīng)有了
三種樣式玩偶的概率相同.某同學已經(jīng)有了![]() 樣式的玩偶,若他再購買兩個這款盲盒,恰好能收集齊這三種樣式的概率是多少?
樣式的玩偶,若他再購買兩個這款盲盒,恰好能收集齊這三種樣式的概率是多少?
(2)某銷售網(wǎng)點為調(diào)查該款盲盒的受歡迎程度,隨機發(fā)放了200份問卷,并全部收回.經(jīng)統(tǒng)計,有![]() 的人購買了該款盲盒,在這些購買者當中,女生占
的人購買了該款盲盒,在這些購買者當中,女生占![]() ;而在未購買者當中,男生女生各占
;而在未購買者當中,男生女生各占![]() .請根據(jù)以上信息填寫下表,并分析是否有
.請根據(jù)以上信息填寫下表,并分析是否有![]() 的把握認為購買該款盲盒與性別有關(guān)?
的把握認為購買該款盲盒與性別有關(guān)?
女生 | 男生 | 總計 | |
購買 | |||
未購買 | |||
總計 |
參考公式: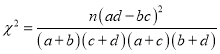 ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)該銷售網(wǎng)點已經(jīng)售賣該款盲盒6周,并記錄了銷售情況,如下表:
周數(shù) | 1 | 2 | 3 | 4 | 5 | 6 |
盒數(shù) | 16 | ______ | 23 | 25 | 26 | 30 |
由于電腦故障,第二周數(shù)據(jù)現(xiàn)已丟失,該銷售網(wǎng)點負責人決定用第4、5、6周的數(shù)據(jù)求線性回歸方程,再用第1、3周數(shù)據(jù)進行檢驗.
①請用4、5、6周的數(shù)據(jù)求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(注: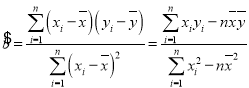 ,
,![]() )
)
②若由線性回歸方程得到的估計數(shù)據(jù)與所選出的檢驗數(shù)據(jù)的誤差均不超過2盒,則認為得到的線性回歸方程是可靠的,試問①中所得的線性回歸方程是否可靠?
③如果通過②的檢驗得到的回歸直線方程可靠,我們可以認為第2周賣出的盒數(shù)誤差也不超過2盒,請你求出第2周賣出的盒數(shù)的可能取值;如果不可靠,請你設計一個估計第2周賣出的盒數(shù)的方案.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知圓![]() 經(jīng)過橢圓
經(jīng)過橢圓![]() 的左右焦點
的左右焦點![]() ,與橢圓
,與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三點共線.
三點共線.
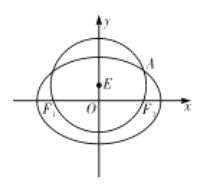
(1)求橢圓![]() 的方程;
的方程;
(2)設與直線![]() (
(![]() 為原點)平行的直線交橢圓
為原點)平行的直線交橢圓![]() 于
于![]() 兩點,當
兩點,當![]() 的面積取取最大值時,求直線
的面積取取最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)).以
為參數(shù)).以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ),將曲線
),將曲線![]() 向左平移2個單位長度得到曲線
向左平移2個單位長度得到曲線![]() .
.
(1)求曲線![]() 的普通方程和極坐標方程;
的普通方程和極坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】謝爾賓斯三角形是一種分形,其具體操作是取一個實心的三角形沿三邊中點的連線,將它分成四個小三角形,去掉中間的那一個小三角形,然后對其余三個小三角形重復以上步驟,得到如下的系列圖稱之為謝爾賓斯:三角形.在第五個圖形中,若隨機的投入一個質(zhì)點,則質(zhì)點落入“空白”處的概率為( )
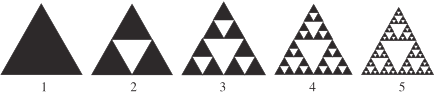
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() 是定義在
是定義在![]() 上的奇函數(shù),且函數(shù)
上的奇函數(shù),且函數(shù)![]() 為偶函數(shù),當
為偶函數(shù),當![]() 時,
時,![]() ,若
,若![]() 有三個零點,則實數(shù)
有三個零點,則實數(shù)![]() 的取值集合是( )
的取值集合是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() 、
、![]() ,求
,求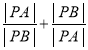 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】圓周率是圓的周長與直徑的比值,一般用字母![]() 表示.我們可以通過設計一個試驗來估計
表示.我們可以通過設計一個試驗來估計![]() 的值:從
的值:從![]() 表示的區(qū)域內(nèi)隨機抽取200個實數(shù)對
表示的區(qū)域內(nèi)隨機抽取200個實數(shù)對![]() ,其中x,y兩個數(shù)能與1構(gòu)成鈍角三角形三邊長的數(shù)對
,其中x,y兩個數(shù)能與1構(gòu)成鈍角三角形三邊長的數(shù)對![]() 共有56個.則用隨機模擬的方法估計
共有56個.則用隨機模擬的方法估計![]() 的近似值為________.
的近似值為________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下圖為國家統(tǒng)計局網(wǎng)站發(fā)布的《2018年國民經(jīng)濟和社會發(fā)展統(tǒng)計公報》中居民消費價格月度漲跌幅度的折線圖(注:同比是今年第![]() 個月與去年第
個月與去年第![]() 個月之比,環(huán)比是現(xiàn)在的統(tǒng)計周期和上一個統(tǒng)計周期之比)
個月之比,環(huán)比是現(xiàn)在的統(tǒng)計周期和上一個統(tǒng)計周期之比)
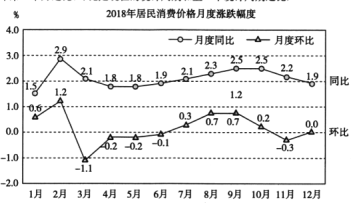
下列說法正確的是( )
①2018年6月CPI環(huán)比下降0.1%,同比上漲1.9%
②2018年3月CPI環(huán)比下降1.1%,同比上漲2.1%
③2018年2月CPI環(huán)比上漲0.6%,同比上漲1.4%
④2018年6月CPI同比漲幅比上月略微擴大1.9個百分點
A.①②B.③④C.①③D.②④.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com