【題目】為了解某校學(xué)生參加社區(qū)服務(wù)的情況，采用按性別分層抽樣的方法進(jìn)行調(diào)查.已知該校共有學(xué)生960人，其中男生560人，從全校學(xué)生中抽取了容量為
的樣本，得到一周參加社區(qū)服務(wù)的時間的統(tǒng)計數(shù)據(jù)如下表：
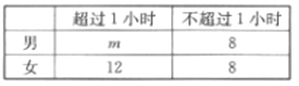
（1）求
，；
（2）能否有
的把握認(rèn)為該校學(xué)生一周參加社區(qū)服務(wù)時間是否超過1小時與性別有關(guān)？
附：
.
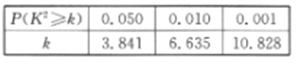
【答案】（1）20,48；（2）沒有.
【解析】
（1）根據(jù)分層抽樣中在各層中的抽樣比相等求得
，然后可得樣本容量
．（2）由題意得到列聯(lián)表，根據(jù)公式求出
后結(jié)合臨界值表中的數(shù)據(jù)可得結(jié)論．
（1）由已知可得該校有女生400人，
根據(jù)題意可得
，解得，
所以
.
（2）由題意得列聯(lián)表如下：
超過1小時的人數(shù) | 不超過1小時的人數(shù) | 合計 | |
男 | 20 | 8 | 28 |
女 | 12 | 8 | 20 |
合計 | 32 | 16 | 48 |
根據(jù)表中的數(shù)據(jù)得
，
所以沒有95%的把握認(rèn)為該校學(xué)生一周參加社區(qū)服務(wù)時間是否超過1小時與性別有關(guān)．
寒假創(chuàng)新型自主學(xué)習(xí)第三學(xué)期寒假銜接系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，直棱柱
的底面是邊長為4的菱形，且
，側(cè)棱長為6， 
，點
分別是線段
的中點.
（1）證明： 
平面
；
（2）求二面角
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知直線
的參數(shù)方程為
(其中
為參數(shù))，以坐標(biāo)原點
為極點，以
軸正半軸為極軸，建立極坐標(biāo)系，曲線
的極坐標(biāo)方程為
（其中
）.
(1)若點
的直角坐標(biāo)為
，且點
在曲線
內(nèi)，求實數(shù)
的取值范圍；
(2)若
,當(dāng)
變化時，求直線
被曲線
截得的弦長的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某校高三文科
名學(xué)生參加了
月份的高考模擬考試，學(xué)校為了了解高三文科學(xué)生的歷史、地理學(xué)習(xí)情況，從名學(xué)生中抽取
名學(xué)生的成績進(jìn)行統(tǒng)計分析，抽出的名學(xué)生的地理、歷史成績?nèi)缦卤恚?/span>
地理 歷史 | [80,100] | [60,80） | [40,60） |
[80,100] | 8 | m | 9 |
[60,80） | 9 | n | 9 |
[40,60） | 8 | 15 | 7 |
若歷史成績在[80,100]區(qū)間的占30%，
（1）求
的值；
（2）請根據(jù)上面抽出的名學(xué)生地理、歷史成績，填寫下面地理、歷史成績的頻數(shù)分布表：
[80,100] | [60,80） | [40,60） | |
地理 | |||
歷史 |
根據(jù)頻數(shù)分布表中的數(shù)據(jù)估計歷史和地理的平均成績及方差（同一組數(shù)據(jù)用該組區(qū)間的中點值作代表），并估計哪個學(xué)科成績更穩(wěn)定.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
．
（1）當(dāng)
時，求函數(shù)
在
上的最小值；
（2）若對任意的
恒成立．試求實數(shù)a的取值范圍；
（3）若
時，求函數(shù)在
上的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在正三棱柱
中，側(cè)棱長和底面邊長均為1， 
是
的中點．
（Ⅰ）求證： 
∥平面
；
（Ⅱ）求
與平面
所成角的正弦值；
（Ⅲ）試問線段
上是否存在點
，使
？若存在，求 
的值，若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在△ABC中，a、b、c分別是角A、B、C的對邊，S是該三角形的面積，且
（1）求角A的大小；
（2）若角A為銳角， 
，求邊BC上的中線AD的長.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某公司發(fā)放員工的薪水有三種方式：①第一個月工資3000元，以后每月以1%的增長率增長；②第一個月工資2400元，以后每月以2%的增長率增長；③第一個月工資為3200元，每月漲工資30元．
（1）設(shè)第x個月的工資分別為
元，試分別建立關(guān)于x的函數(shù)；
（2）借助計算器計算這三種情況下各個月的工資；
（3）請分析這三種領(lǐng)薪方法的區(qū)別，作為員工選擇何種方法更合算？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知雙曲線
=1，P為雙曲線右支上除x軸上之外的一點．
（1）若∠F1PF2=θ，求△F1PF2的面積．
（2）若該雙曲線與橢圓
+y2=1有共同的焦點且過點A（2，1），求△F1PF2內(nèi)切圓的圓心軌跡方程．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com