【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點．研究表明：“活水圍網”養魚時，某種魚在一定的條件下，每尾魚的平均生長速度
（單位：千克/年）是養殖密度
（單位：尾/立方米）的函數．當不超過4（尾/立方米）時，的值為
（千克/年）；當
時，
是
的一次函數；當達到
（尾/立方米）時，因缺氧等原因，的值為
（千克/年）．
（1）當
時，求函數
的表達式；
（2）當養殖密度為多大時，魚的年生長量（單位：千克/立方米）
可以達到最大，并求出最大值．
科目：高中數學 來源： 題型：
【題目】我國古代數學家劉徽是公元三世紀世界上最杰出的數學家，他在《九章算術圓田術》注中，用割圓術證明了圓面積的精確公式，并給出了計算圓周率的科學方法.所謂“割圓術”，即通過圓內接正多邊形細割圓，并使正多邊形的周長無限接近圓的周長，進而來求得較為精確的圓周率（圓周率指圓周長與該圓直徑的比率）.劉徽計算圓周率是從正六邊形開始的，易知圓的內接正六邊形可分為六個全等的正三角形，每個三角形的邊長均為圓的半徑
，此時圓內接正六邊形的周長為
，此時若將圓內接正六邊形的周長等同于圓的周長，可得圓周率為3，當用正二十四邊形內接于圓時，按照上述算法，可得圓周率為__________．（參考數據： 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
經過點
，且離心率為
．
（Ⅰ）求橢圓
的方程；
（Ⅱ）設
是橢圓上的點，直線
與
（
為坐標原點）的斜率之積為
．若動點
滿足
，試探究是否存在兩個定點
，使得
為定值？若存在，求的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】端午節吃粽子是我國的傳統習俗．設一盤中裝有10個粽子，其中豆沙粽2個，肉粽3個，白粽5個，這三種粽子的外觀完全相同．從中任意選取3個.
(1)求三種粽子各取到1個的概率；
(2)設X表示取到的豆沙粽個數，求X的分布列與數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy上取兩個定點
再取兩個動點
，
，且
．
（Ⅰ）求直線
與
交點M的軌跡C的方程；
（Ⅱ）過
的直線與軌跡C交于P,Q，過P作
軸且與軌跡C交于另一點N，F為軌跡C的右焦點，若
,求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】生活經驗告訴我們，當水注進容器(設單位時間內進水量相同)時，水的高度隨著時間的變化而變化，在下圖中請選擇與容器相匹配的圖像，A對應________；B對應________；C對應________；D對應________．
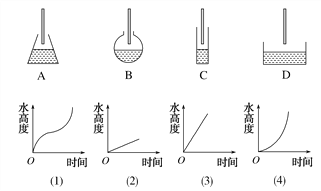
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量指數（
，簡稱
）是定量描述空氣質量狀況的無量綱指數，參與空氣質量評價的主要污染物為
等六項.空氣質量按照大小分為六級：一級
為優；二級
為良好；三級
為輕度污染；四級
為中度污染；五級
為重度污染；六級
為嚴重污染.
某人根據環境監測總站公布的數據記錄了某地某月連續10天的莖葉圖如圖所示：
（1）利用訪樣本估計該地本月空氣質量優良（
）的天數；（按這個月總共30天計算）；
（2）若從樣本中的空氣質量不佳（
）的這些天中，隨機地抽取三天深入分析各種污染指標，求這三天的空氣質量等級互不相同的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，AE⊥DE，CD⊥平面ADE，AB⊥平面ADE，CD=DA=6，AB=2，DE=3．
（1）求
到平面
的距離
（2）在線段
上是否存在一點
，使
？若存在，求出
的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知長方形ABCD中，AB＝3，AD＝4.現將長方形沿對角線BD折起，使AC＝a，得到一個四面體A－BCD，如圖所示.
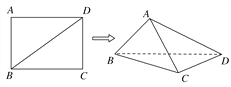
(1)試問：在折疊的過程中，直線AB與CD能否垂直？若能，求出相應a的值；若不能，請說明理由；
(2)求四面體A－BCD體積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
