
【題目】已知函數![]() ,實數
,實數![]() 為常數).
為常數).
(1)若![]() ,且函數
,且函數![]() 在
在![]() 上的最小值為0,求
上的最小值為0,求![]() 的值;
的值;
(2)若對于任意的實數![]() ,函數
,函數![]() 在區間
在區間![]() 上總是減函數,對每個給定的
上總是減函數,對每個給定的![]() ,求
,求![]() 的最大值
的最大值![]() .
.
【答案】(1)![]() ;(2)
;(2)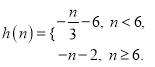 .
.
【解析】試題分析:(1)先求導,求函數在已知區間上的極值,注意極值點是否在定義域內,進行分類討論,確定最小值,列出關于![]() 的方程即可得結果;(2)函數在區間上單調遞減,轉化為導函數小于等于0恒成立,再轉化為二次函數根的分布問題.
的方程即可得結果;(2)函數在區間上單調遞減,轉化為導函數小于等于0恒成立,再轉化為二次函數根的分布問題.
試題解析:(1)當![]() 時,
時, ![]() .
.
則![]() .
.
令![]() ,得
,得![]() (舍),
(舍),![]() .
.
①當![]() >1時,
>1時,
| 1 |
|
|
|
| - | 0 | + | |
|
| ↘ |
| ↗ |
∴當![]() 時,
時, ![]() .
.
令![]() ,得
,得![]() .
.
②當![]() 時,
時, ![]() ≥0在
≥0在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上為增函數,當
上為增函數,當![]() 時,
時, ![]() .
.
令![]() ,得
,得![]() (舍).
(舍).
綜上所述,所求![]() 為
為![]() .
.
(2) ∵對于任意的實數![]() ,
, ![]() ,
, ![]() 在區間
在區間![]() 上總是減函數,
上總是減函數,
則對于x∈(1,3), ![]() <0,
<0,
∴![]() 在區間[1,3]上恒成立.
在區間[1,3]上恒成立.
設g(x)= ![]() ,∵
,∵![]() ,∴g(x)
,∴g(x) ![]() 在區間[1,3]上恒成立.
在區間[1,3]上恒成立.
由g(x)二次項系數為正,得
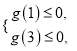 即
即![]() 亦即
亦即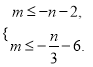
∵![]()
![]() =
=![]() ,
,
∴ 當n<6時,m≤![]() ,當n≥6時,m≤
,當n≥6時,m≤![]() ,
,
∴ 當n<6時,h(n)= ![]() ,當n≥6時,h(n)=
,當n≥6時,h(n)= ![]() ,
,
即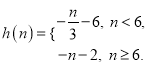


科目:高中數學 來源: 題型:
【題目】設關于x的一元二次方程x2+2ax+b2=0.
(1)若a是從0,1,2,3四個數中任取的一個數,b是從0,1,2三個數中任取的一個數,求上述方程有實根的概率.
(2)若a是從區間[0,3]任取的一個數,b是從區間[0,2]任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩所學校高三年級分別有1 200人,1 000人,為了了解兩所學校全體高三年級學生在該地區六校聯考的數學成績情況,采用分層抽樣方法從兩所學校一共抽取了110名學生的數學成績,并作出了頻數分布統計表如下:
甲校:
分組 | [70,80) | [80,90) | [90,100) | [100,110) |
頻數 | 3 | 4 | 8 | 15 |
分組 | [110,120) | [120,130) | [130,140) | [140,150] |
頻數 | 15 | x | 3 | 2 |
乙校:
分組 | [70,80) | [80,90) | [90,100) | [100,110) |
頻數 | 1 | 2 | 8 | 9 |
分組 | [110,120) | [120,130) | [130,140) | [140,150] |
頻數 | 10 | 10 | y | 3 |
則x,y的值分別為( )
(A)、12,7 (B)、 10,7 (C)、 10,8 (D)、 11,9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點.從A點測得 M點的仰角∠MAN=60°,C點的仰角∠CAB=45°以及∠MAC=75°;從C點測得∠MCA=60°.已知山高BC=100m,則山高MN=m. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三角形的頂點分別為A(﹣1,3),B(3,2),C(1,0)
(1)求BC邊上高的長度;
(2)若直線l過點C,且在l上不存在到A,B兩點的距離相等的點,求直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com