
【題目】已知函數(shù)f(x)=x|2x﹣a|﹣1.
①當(dāng)a=0時,不等式f(x)+1>0的解集為_____;
②若函數(shù)f(x)有三個不同的零點(diǎn),則實(shí)數(shù)a的取值范圍是_____.
【答案】(0,+∞) (2![]() ,+∞)
,+∞)
【解析】
①把a=0代入函數(shù)解析式,可得不等式,對x分類求解得答案;
②轉(zhuǎn)化方程的根為兩個函數(shù)的圖象的交點(diǎn),利用數(shù)形結(jié)合,通過函數(shù)的導(dǎo)數(shù)求解即可.
①當(dāng)a=0時,不等式f(x)+1>0x|2x|﹣1+1>0,
即2x|x|>0,
若x<0,得﹣2x2>0,不合題意;
若x=0,得0>0,不合題意;
若x>0,得2x2>0,則x>0.
綜上,當(dāng)a=0時,不等式f(x)+1>0的解集為(0,+∞);
②若函數(shù)f(x)有三個不同的零點(diǎn),即方程x|2x﹣a|﹣1=0有3個不同根.
即|2x﹣a|![]() 有三個解,
有三個解,
令y=|2x﹣a|,則y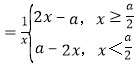 ,畫出兩個函數(shù)的圖象,如圖:
,畫出兩個函數(shù)的圖象,如圖:
x![]() ,y
,y![]() ,由y′
,由y′![]() 2,解得x
2,解得x![]() ,x
,x![]() (舍去),
(舍去),
此時切點(diǎn)坐標(biāo)(![]() ),代入y=a﹣2x,可得a=2
),代入y=a﹣2x,可得a=2![]() 2
2![]() ,
,
函數(shù)f(x)=x|2x﹣a|﹣1有三個零點(diǎn),
則實(shí)數(shù)a的取值范圍為(2![]() ,+∞).
,+∞).
故答案為:(0,+∞);(2![]() ,+∞).
,+∞).


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(![]() )若
)若![]() 在
在![]() 處取得極值,求實(shí)數(shù)
處取得極值,求實(shí)數(shù)![]() 的值.
的值.
(![]() )求函數(shù)
)求函數(shù)![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
(![]() )若
)若![]() 在
在![]() 上沒有零點(diǎn),求實(shí)數(shù)
上沒有零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (a為常數(shù))的圖象與
(a為常數(shù))的圖象與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線斜率為
處的切線斜率為![]()
(1)求![]() 的值及函數(shù)
的值及函數(shù)![]() 的極值;
的極值;
(2)證明:當(dāng)![]() 時,
時,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正方形![]() 的對角線
的對角線![]() 與
與![]() 相交于
相交于![]() 點(diǎn),將
點(diǎn),將![]() 沿對角線折起,使得平面
沿對角線折起,使得平面![]() 平面
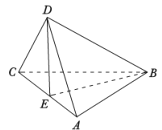
平面![]() (如圖),則下列命題中正確的是( )
(如圖),則下列命題中正確的是( )
A. 直線![]() 直線
直線![]() ,且直線
,且直線![]() 直線
直線![]()
B. 直線![]() 平面
平面![]() ,且直線
,且直線![]() 平面
平面![]()
C. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
D. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合M={(x,y)|y=f(x)},若對于任意實(shí)數(shù)對(x1,y1)∈M,存在(x2,y2)∈M,使x1x2+y1y2=0成立,則稱集合M具有∟性,給出下列四個集合:
①M(fèi)={(x,y)|y=x3﹣2x2+3}; ②M={(x,y)|y=log2(2﹣x)};
③M={(x,y)|y=2﹣2x}; ④M={(x,y)|y=1﹣sinx};
其中具有∟性的集合的個數(shù)是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在汶川大地震后對唐家山堰塞湖的搶險(xiǎn)過程中,武警官兵準(zhǔn)備用射擊的方法引爆從湖壩上游漂流而下的一個巨大的汽油罐.已知只有5發(fā)子彈,第一次命中只能使汽油流出,第二次命中才能引爆.每次射擊是相互獨(dú)立的,且命中的概率都是 ![]() .
.
(1)求油罐被引爆的概率;
(2)如果引爆或子彈打光則停止射擊,設(shè)射擊次數(shù)為ξ.求ξ的分布列及數(shù)學(xué)期望E(ξ).( 結(jié)果用分?jǐn)?shù)表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() ,直線y=
,直線y= ![]() x為曲線y=f(x)的切線(e為自然對數(shù)的底數(shù)).
x為曲線y=f(x)的切線(e為自然對數(shù)的底數(shù)).
(1)求實(shí)數(shù)a的值;
(2)用min{m,n}表示m,n中的最小值,設(shè)函數(shù)g(x)=min{f(x),x﹣ ![]() }(x>0),若函數(shù)h(x)=g(x)﹣cx2為增函數(shù),求實(shí)數(shù)c的取值范圍.
}(x>0),若函數(shù)h(x)=g(x)﹣cx2為增函數(shù),求實(shí)數(shù)c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a>0且a≠1,若函數(shù)f(x)=loga[ax2﹣(2﹣a)x+3]在[ ![]() ,2]上是增函數(shù),則a的取值范圍是 .
,2]上是增函數(shù),則a的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖, ![]() 為坐標(biāo)原點(diǎn),雙曲線
為坐標(biāo)原點(diǎn),雙曲線![]() 和橢圓
和橢圓![]() 均過點(diǎn)
均過點(diǎn) ,且以
,且以![]() 的兩個頂點(diǎn)和
的兩個頂點(diǎn)和![]() 的兩個焦點(diǎn)為頂點(diǎn)的四邊形是面積為2的正方形.
的兩個焦點(diǎn)為頂點(diǎn)的四邊形是面積為2的正方形.

(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() ,使得
,使得![]() 與
與![]() 交于
交于![]() 兩點(diǎn),與
兩點(diǎn),與![]() 只有一個公共點(diǎn),且
只有一個公共點(diǎn),且![]() ?證明你的結(jié)論.
?證明你的結(jié)論.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com