
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點
的中點![]() 是由
是由![]() 繞直線
繞直線![]() 旋轉得到,連結
旋轉得到,連結![]() ,
,![]() ,
,![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
【題目】己知橢圓![]() 過點
過點![]() ,
,![]() ,
,![]() 是兩個焦點.以橢圓
是兩個焦點.以橢圓![]() 的上頂點
的上頂點![]() 為圓心作半徑為
為圓心作半徑為![]() 的圓,
的圓,
(1)求橢圓![]() 的方程;
的方程;
(2)存在過原點的直線![]() ,與圓
,與圓![]() 分別交于
分別交于![]() ,
,![]() 兩點,與橢圓
兩點,與橢圓![]() 分別交于
分別交于![]() ,
,![]() 兩點(點
兩點(點![]() 在線段
在線段![]() 上),使得
上),使得![]() ,求圓
,求圓![]() 半徑
半徑![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為了提高生產效率,對生產設備進行了技術改造,為了對比技術改造后的效果,采集了技術改造前后各20次連續正常運行的時間長度(單位:天)數據,整理如下:
改造前:19,31,22,26,34,15,22,25,40,35,18,16,28,23,34,15,26,20,24,21
改造后:32,29,41,18,26,33,42,34,37,39,33,22,42,35,43,27,41,37,38,36
(1)完成下面的列聯表,并判斷能否有99%的把握認為技術改造前后的連續正常運行時間有差異?
超過30 | 不超過30 | |
改造前 | ||
改造后 |
(2)工廠的生產設備的運行需要進行維護,工廠對生產設備的生產維護費用包括正常維護費,保障維護費兩種.對生產設備設定維護周期為T天(即從開工運行到第kT天,k∈N*)進行維護.生產設備在一個生產周期內設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內,若生產設備能連續運行,則只產生一次正常維護費,而不會產生保障維護費;若生產設備不能連續運行,則除產生一次正常維護費外,還產生保障維護費.經測算,正常維護費為0.5萬元/次;保障維護費第一次為0.2萬元/周期,此后每增加一次則保障維護費增加0.2萬元.現制定生產設備一個生產周期(以120天計)內的維護方案:T=30,k=1,2,3,4.以生產設備在技術改造后一個維護周期內能連續正常運行的頻率作為概率,求一個生產周期內生產維護費的分布列及均值.
附: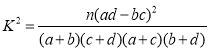
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一條曲線C在y軸右側,曲線C上任意一點到點![]() 的距離減去它到y軸的距離都等于1.
的距離減去它到y軸的距離都等于1.
(1)求曲線C的方程;
(2)直線![]() 與軌跡C交于A,B兩點,問:在x軸上是否存在定點
與軌跡C交于A,B兩點,問:在x軸上是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 關于x軸對稱而與直線
關于x軸對稱而與直線![]() 的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )過點
)過點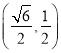 ,離心率為
,離心率為![]() .其左、右焦點分別為
.其左、右焦點分別為![]() ,
,![]() ,O為坐標原點.直線l:
,O為坐標原點.直線l:![]() 與以線段
與以線段![]() 為直徑的圓相切,且直線l與橢圓C交于不同的A,B兩點.
為直徑的圓相切,且直線l與橢圓C交于不同的A,B兩點.
(1)求橢圓C的方程;
(2)若滿足![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的多面體ABCDEF滿足:正方形ABCD與正三角形FBC所在的兩個平面互相垂直,FB∥AE且FB=2EA.
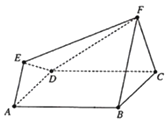
(1)證明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全球抗擊新冠肺炎疫情期間,我國醫療物資生產企業加班加點生產口罩、防護服、消毒水等防疫物品,保障抗疫一線醫療物資供應,在國際社會上贏得一片贊譽.我國某口罩生產企業在加大生產的同時,狠抓質量管理,不定時抽查口罩質量,該企業質檢人員從所生產的口罩中隨機抽取了100個,將其質量指標值分成以下六組:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,得到如下頻率分布直方圖.
,得到如下頻率分布直方圖.
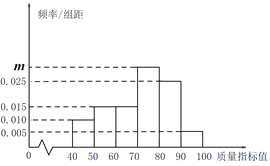
(1)求出直方圖中![]() 的值;
的值;
(2)利用樣本估計總體的思想,估計該企業所生產的口罩的質量指標值的平均數和中位數(同一組中的數據用該組區間中點值作代表,中位數精確到0.01);
(3)現規定:質量指標值小于70的口罩為二等品,質量指標值不小于70的口罩為一等品.利用分層抽樣的方法從該企業所抽取的100個口罩中抽出5個口罩,并從中再隨機抽取2個作進一步的質量分析,試求這2個口罩中恰好有1個口罩為一等品的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com