
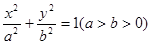 ,左焦點
,左焦點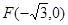 ,且離心率
,且離心率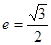
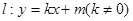 與橢圓C交于不同的兩點
與橢圓C交于不同的兩點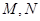 (
(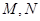 不是左、右頂點),且以
不是左、右頂點),且以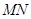 為直徑的圓經(jīng)過橢圓C的右頂點A. 求證:直線
為直徑的圓經(jīng)過橢圓C的右頂點A. 求證:直線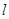 過定點,并求出定點的坐標(biāo).
過定點,并求出定點的坐標(biāo).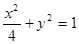 (2) 直線
(2) 直線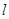 過定點,且定點的坐標(biāo)為
過定點,且定點的坐標(biāo)為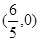
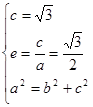 ……1分
……1分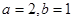 ………2分
………2分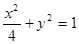 ……3分
……3分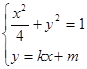
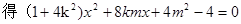 …4分
…4分
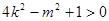 ………..5分
………..5分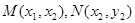
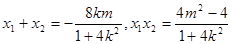 …….6分
…….6分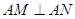 且橢圓的右頂點為
且橢圓的右頂點為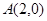 ………7分
………7分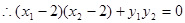 ……… 8分
……… 8分 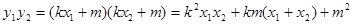
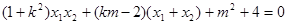
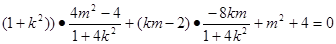 …… 10分
…… 10分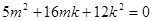 ……11分
……11分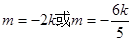 均滿足
均滿足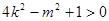 ……12分
……12分
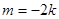 時,直線的
時,直線的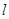 方程為
方程為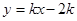 ,過定點(2,0)與題意矛盾舍去……13分
,過定點(2,0)與題意矛盾舍去……13分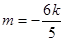 時,直線的
時,直線的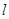 方程為
方程為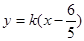 ,過定點
,過定點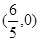
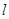 過定點,且定點的坐標(biāo)為
過定點,且定點的坐標(biāo)為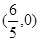 …….14分
…….14分

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 :
: (
( )的離心率為
)的離心率為 ,過右焦點
,過右焦點 且斜率為1的直線交橢圓
且斜率為1的直線交橢圓 于
于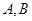 兩點,
兩點, 為弦
為弦 的中點。
的中點。 (
( 為坐標(biāo)原點)的斜率
為坐標(biāo)原點)的斜率 ;
; 橢圓
橢圓 上任意一點,且
上任意一點,且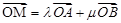 ,求
,求 的最大值和最小值.
的最大值和最小值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 的中心在原點,焦點在
的中心在原點,焦點在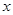 軸上,一條經(jīng)過點
軸上,一條經(jīng)過點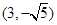 且方向向量為
且方向向量為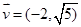 的直線
的直線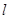 交橢圓
交橢圓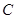 于
于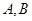 兩點,交
兩點,交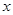 軸于
軸于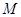 點,且
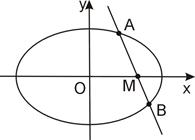
點,且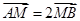 .
.
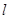 的方程;
的方程; 長軸長的取值范圍.
長軸長的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
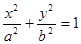 (
(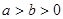 )過點
)過點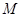 (0,2),離心率
(0,2),離心率 .
.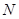 (2,0)的直線
(2,0)的直線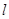 與橢圓相交于
與橢圓相交于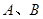 兩點,且
兩點,且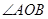 為銳角(其中
為銳角(其中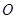 為坐標(biāo)原點),求直線
為坐標(biāo)原點),求直線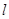 斜率的取值范圍.
斜率的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
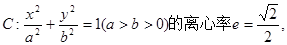 左、右焦點分別為F1、F2,點
左、右焦點分別為F1、F2,點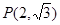 ,點F2在線段PF1的中垂線上。
,點F2在線段PF1的中垂線上。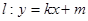 與橢圓C交于M、N兩點,直線F2M與F2N的傾斜角互補(bǔ),求證:直線
與橢圓C交于M、N兩點,直線F2M與F2N的傾斜角互補(bǔ),求證:直線 過定點,并求該定點的坐標(biāo)。
過定點,并求該定點的坐標(biāo)。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
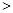 0)的焦點F的直線交拋物線于點A、B,交其準(zhǔn)線于點C,若|BC|=2|BF|,且|AF|=3.則此拋物線的方程為( )
0)的焦點F的直線交拋物線于點A、B,交其準(zhǔn)線于點C,若|BC|=2|BF|,且|AF|=3.則此拋物線的方程為( )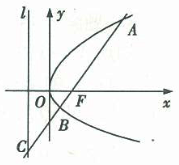
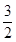 x
x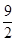 x
x查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 :
: 的右焦點為F,離心率
的右焦點為F,離心率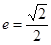 ,橢圓C上的點到F的距離的最大值為
,橢圓C上的點到F的距離的最大值為 ,直線l過點F與橢圓C交于不同的兩點A、B.
,直線l過點F與橢圓C交于不同的兩點A、B.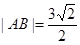 ,求直線l的方程.
,求直線l的方程.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
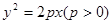 的焦點為
的焦點為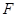 ,其上的動點
,其上的動點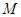 在準(zhǔn)線上的射影為
在準(zhǔn)線上的射影為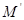 ,若
,若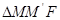 是等邊三角形,則
是等邊三角形,則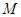 的橫坐標(biāo)是( )
的橫坐標(biāo)是( )A.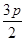 | B.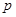 | C.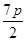 | D.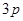 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com