
【題目】設![]() ,函數
,函數![]() .
.
(Ⅰ)討論函數![]() 的單調區間和極值;
的單調區間和極值;
(Ⅱ)已知![]() (
(![]() 是自然對數的底數)和
是自然對數的底數)和![]() 是函數
是函數![]() 的兩個不同的零點,求
的兩個不同的零點,求![]() 的值并證明:
的值并證明:![]() .
.
【答案】(Ⅰ)①當![]() 時,函數
時,函數![]() 的遞增區間為
的遞增區間為![]() ,無極值,②當
,無極值,②當![]() 時,函數
時,函數![]() 的遞增區間為
的遞增區間為![]() ,遞減區間是
,遞減區間是![]() ,函數
,函數![]() 的極大值為
的極大值為![]() ;(Ⅱ)證明見解析.
;(Ⅱ)證明見解析.
【解析】
試題(Ⅰ)分別令![]() 及
及![]() 分情況討論;(Ⅱ)由已知得
分情況討論;(Ⅱ)由已知得![]() ,由(Ⅰ)函數
,由(Ⅰ)函數![]() 在
在![]() 遞減及
遞減及![]() ,
,![]() ,可知函數
,可知函數![]() 在區間
在區間![]() 有唯一零點,由此得證.
有唯一零點,由此得證.
試題解析:(Ⅰ)由已知得![]()
![]() ,
,![]() ,
,
①若![]() ,則
,則![]() ,
,![]() 是區間
是區間![]() 上的增函數,無極值;
上的增函數,無極值;
②若![]() ,令
,令![]() ,得
,得![]() ,
,
在區間![]() 上,
上,![]() ,函數
,函數![]() 是增函數,
是增函數,
在區間![]() 上,
上,![]() ,函數
,函數![]() 是減函數,
是減函數,
所以在區間![]() 上,
上,![]() 的極大值為
的極大值為![]() .
.
綜上所述,①當![]() 時,函數
時,函數![]() 的遞增區間為
的遞增區間為![]() ,無極值;②當
,無極值;②當![]() 時,函數
時,函數![]() 的遞增區間為
的遞增區間為![]() ,遞減區間是
,遞減區間是![]() ,函數
,函數![]() 的極大值為
的極大值為![]() .
.
(Ⅱ)因為![]() ,所以
,所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,
由(Ⅰ)函數![]() 在
在![]() 遞減,故函數
遞減,故函數![]() 在區間
在區間![]() 有唯一零點,因此
有唯一零點,因此![]() .
.


科目:高中數學 來源: 題型:
【題目】一種新的驗血技術可以提高血液檢測效率.現某專業檢測機構提取了![]() 份血液樣本,其中只有1份呈陽性,并設計了如下混合檢測方案:先隨機對其中
份血液樣本,其中只有1份呈陽性,并設計了如下混合檢測方案:先隨機對其中![]() 份血液樣本分別取樣,然后再混合在一起進行檢測,若檢測結果為陰性,則對另外3份血液逐一檢測,直到確定呈陽性的血液為止;若檢測結果呈陽性,測對這
份血液樣本分別取樣,然后再混合在一起進行檢測,若檢測結果為陰性,則對另外3份血液逐一檢測,直到確定呈陽性的血液為止;若檢測結果呈陽性,測對這![]() 份血液再逐一檢測,直到確定呈陽性的血液為止.
份血液再逐一檢測,直到確定呈陽性的血液為止.
(1)若![]() ,求恰好經過3次檢測而確定呈陽性的血液的事件概率;
,求恰好經過3次檢測而確定呈陽性的血液的事件概率;
(2)若![]() ,宜采用以上方案檢測而確定呈陽性的血液所需次數為
,宜采用以上方案檢測而確定呈陽性的血液所需次數為![]() ,
,
①求![]() 的概率分布;
的概率分布;
②求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】兩個同樣的紅球、兩個同樣的黑球和兩個同樣的白球放入下列6個格中,要求同種顏色的球不相鄰,則可能的放球方法共有______種.(用數字作答)
1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位在2019年重陽節組織50名退休職工(男、女各25名)旅游,退休職工可以選擇到甲、乙兩個景點其中一個去旅游.他們最終選擇的景點的結果如下表:
男性 | 女性 | |
甲景點 | 20 | 10 |
乙景點 | 5 | 15 |
(1)據此資料分析,是否有![]() 的把握認為選擇哪個景點與性別有關?
的把握認為選擇哪個景點與性別有關?
(2)按照游覽不同景點用分層抽樣的方法,在女職工中選取5人,再從這5人中隨機抽取2人進行采訪,求這2人游覽的景點不同的概率.
附: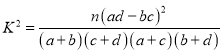 ,
,![]() .
.
P( | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,圓
為坐標原點,圓![]() :
:![]() ,定點
,定點![]() ,點
,點![]() 是圓
是圓![]() 上一動點,線段
上一動點,線段![]() 的垂直平分線交圓
的垂直平分線交圓![]() 的半徑
的半徑![]() 于點
于點![]() ,點
,點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)不垂直于![]() 軸且不過
軸且不過![]() 點的直線
點的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,若直線
兩點,若直線![]() 、
、![]() 的斜率之和為0,則動直線
的斜率之和為0,則動直線![]() 是否一定經過一定點?若過一定點,則求出該定點的坐標;若不過定點,請說明理由.
是否一定經過一定點?若過一定點,則求出該定點的坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知多面體ABCDEF中,四邊形ABFE為正方形,![]() ,
,![]() ,G為AB的中點,
,G為AB的中點,![]() .
.
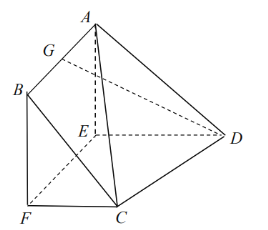
(1)求證:![]() 平面CDEF;
平面CDEF;
(2)求平面ACD與平面BCF所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與橢圓
與橢圓![]() 相交于點M(0,1),N(0,-1),且橢圓的離心率為
相交于點M(0,1),N(0,-1),且橢圓的離心率為![]() .
.
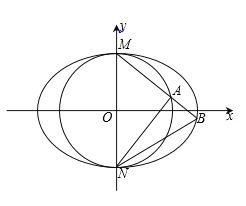
(1)求![]() 的值和橢圓C的方程;
的值和橢圓C的方程;
(2)過點M的直線![]() 交圓O和橢圓C分別于A,B兩點.
交圓O和橢圓C分別于A,B兩點.
①若![]() ,求直線
,求直線![]() 的方程;
的方程;
②設直線NA的斜率為![]() ,直線NB的斜率為
,直線NB的斜率為![]() ,問:
,問:![]() 是否為定值? 如果是,求出定值;如果不是,說明理由.
是否為定值? 如果是,求出定值;如果不是,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com