
【題目】已知函數(shù)![]() ,若存在實數(shù)
,若存在實數(shù)![]() ,使得對于定義域內(nèi)的任意實數(shù)
,使得對于定義域內(nèi)的任意實數(shù)![]() ,均有
,均有![]() 成立,則稱函數(shù)
成立,則稱函數(shù)![]() 為“可平衡”函數(shù),有序數(shù)對
為“可平衡”函數(shù),有序數(shù)對![]() 稱為函數(shù)
稱為函數(shù)![]() 的“平衡”數(shù)對.
的“平衡”數(shù)對.
(1)若![]() ,判斷
,判斷![]() 是否為“可平衡”函數(shù),并說明理由;
是否為“可平衡”函數(shù),并說明理由;
(2)若![]() ,
,![]() ,當
,當![]() 變化時,求證:
變化時,求證:![]() 與
與![]() 的“平衡”數(shù)對相同;
的“平衡”數(shù)對相同;
(3)若![]() ,且
,且![]() 、
、![]() 均為函數(shù)
均為函數(shù)![]() 的“平衡”數(shù)對.當
的“平衡”數(shù)對.當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 是“可平衡”函數(shù),詳見解析(2)證明見解析(3)
是“可平衡”函數(shù),詳見解析(2)證明見解析(3)![]()
【解析】
(1)利用兩角和差的正弦公式求解即可.
(2)根據(jù)題意可知,對于任意實數(shù)![]() ,
,![]() ,再列式利用恒成立問題求解即可.
,再列式利用恒成立問題求解即可.
(3)根據(jù)“平衡數(shù)對”的定義將![]() 用關(guān)于
用關(guān)于![]() 的三角函數(shù)表達,再利用三角函數(shù)的取值范圍求解即可.
的三角函數(shù)表達,再利用三角函數(shù)的取值范圍求解即可.
(1)若![]() ,則
,則![]() ,
,
![]()
![]() ,
,
要使得![]() 為“可平衡”函數(shù),需使故
為“可平衡”函數(shù),需使故![]() 對于任意實數(shù)
對于任意實數(shù)![]() 均成立,只有
均成立,只有![]() ,
,
此時![]() ,
,![]() ,故
,故![]() 存在,所以
存在,所以![]() 是“可平衡”函數(shù).
是“可平衡”函數(shù).
(2)![]() 及
及![]() 的定義域均為
的定義域均為![]() ,
,
根據(jù)題意可知,對于任意實數(shù)![]() ,
,![]() ,
,
即![]() ,即
,即![]() 對于任意實數(shù)
對于任意實數(shù)![]() 恒成立,
恒成立,
只有![]() ,
,![]() ,故函數(shù)
,故函數(shù)![]() 的“平衡”數(shù)對為
的“平衡”數(shù)對為![]() ,
,
對于函數(shù)![]() 而言,
而言,![]()
![]() ,
,
所以![]() ,
,
![]() ,
,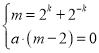 ,
,
即![]() ,故
,故![]() ,只有
,只有![]() ,所以函數(shù)
,所以函數(shù)![]() 的“平衡”數(shù)對為
的“平衡”數(shù)對為![]() ,
,
綜上可得函數(shù)![]() 與
與![]() 的“平衡”數(shù)對相同.
的“平衡”數(shù)對相同.
(3)![]() ,所以
,所以![]() ,
,
![]() ,所以
,所以![]() ,
,
由于![]() ,所以
,所以![]() ,故
,故![]() ,
,![]() ,
,
![]()
![]() ,
,
由于![]() ,所以
,所以![]() 時,
時,![]() ,
,
![]() ,所以
,所以![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知集合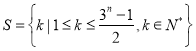 (
(![]() ,且
,且![]() ),若存在非空集合
),若存在非空集合![]() ,使得
,使得![]() ,且
,且![]() ,并任意
,并任意![]() ,都有
,都有![]() ,則稱集合S具有性質(zhì)P,
,則稱集合S具有性質(zhì)P,![]() 稱為集合S的P子集.
稱為集合S的P子集.
(1)當![]() 時,試說明集合S具有性質(zhì)P,并寫出相應(yīng)的P子集
時,試說明集合S具有性質(zhì)P,并寫出相應(yīng)的P子集![]() ;
;
(2)若集合S具有性質(zhì)P,集合T是集合S的一個P子集,設(shè)![]() ,求證:任意
,求證:任意![]() ,
,![]() ,都有
,都有![]() ;
;
(3)求證:對任意正整數(shù)![]() ,集合S具有性質(zhì)P.
,集合S具有性質(zhì)P.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】我國已進入新時代中國特色社會主義時期,人民生活水平不斷提高.某市隨機統(tǒng)計了城區(qū)若干戶市民十月人均生活支出比九月人均生活支出增加量(記為P元)的情況,并根據(jù)統(tǒng)計數(shù)據(jù)制成如圖頻率分布直方圖.
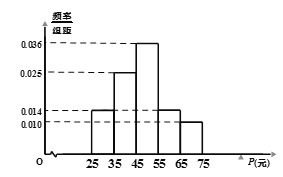
(1)根據(jù)頻率分布直方圖估算P的平均值![]() ;
;
(2)若該市城區(qū)有4戶市民十月人均生活支出比九月人均生活支出分別增加了42元,50元,52元,60元,從這4戶中隨機抽取2戶,求這2戶P值的和超過100元的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形, ![]() 平面
平面![]() ,
,![]() ,E,F分別是
,E,F分別是![]() ,
,![]() 的中點.
的中點.
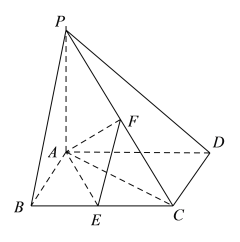
(1)求證:![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】數(shù)列![]() 的前
的前![]() 項和為
項和為![]() 且滿足
且滿足![]() ,
,![]() (
(![]() 為常數(shù),
為常數(shù),![]() ).
).
(1)求![]() ;
;
(2)若數(shù)列![]() 是等比數(shù)列,求實數(shù)
是等比數(shù)列,求實數(shù)![]() 的值;
的值;
(3)是否存在實數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 滿足:可以從中取出無限多項并按原來的先后次序排成一個等差數(shù)列?若存在,求出所有滿足條件的值;若不存在,請說明理由.
滿足:可以從中取出無限多項并按原來的先后次序排成一個等差數(shù)列?若存在,求出所有滿足條件的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“團購”已經(jīng)滲透到我們每個人的生活,這離不開快遞行業(yè)的發(fā)展,下表是2013-2017年全國快遞業(yè)務(wù)量(x億件:精確到0.1)及其增長速度(y%)的數(shù)據(jù)
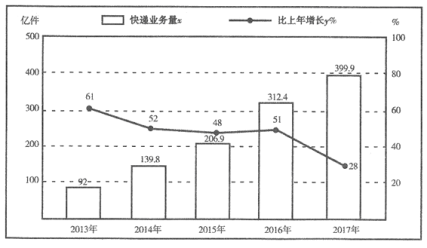
(1)試計算2012年的快遞業(yè)務(wù)量;
(2)分別將2013年,2014年,…,2017年記成年的序號t:1,2,3,4,5;現(xiàn)已知y與t具有線性相關(guān)關(guān)系,試建立y關(guān)于t的回歸直線方程![]() ;
;
(3)根據(jù)(2)問中所建立的回歸直線方程,估算2019年的快遞業(yè)務(wù)量
附:回歸直線的斜率和截距地最小二乘法估計公式分別為: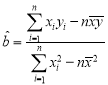 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1所示,在直角梯形DCEF中,![]() ,
,![]() ,
,![]() ,
,![]() ,將四邊形ABEF沿AB邊折成圖2.
,將四邊形ABEF沿AB邊折成圖2.
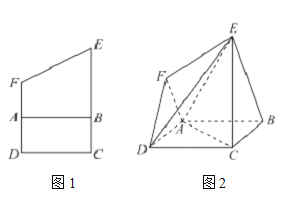
(1)求證:![]() 平面DEF;
平面DEF;
(2)若![]() ,求平面DEF與平面EAC所成銳二面角的余弦值.
,求平面DEF與平面EAC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的焦點在圓
的焦點在圓![]() 上,且橢圓上一點與兩焦點圍成的三角形周長為
上,且橢圓上一點與兩焦點圍成的三角形周長為![]() .
.
(1)求橢圓的方程;
(2)過圓![]() 上一點作圓的切線
上一點作圓的切線![]() 交橢圓于
交橢圓于![]() 兩點,證明:點
兩點,證明:點![]() 在以
在以![]() 為直徑的圓內(nèi).
為直徑的圓內(nèi).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com