
【題目】已知直線l的方程為(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.
(1)求證:直線l恒過定點;
(2)當m變化時,求點P(3,1)到直線l的距離的最大值;
(3)若直線l分別與x軸、y軸的負半軸交于A,B兩點,求△AOB面積的最小值及此時直線l的方程.
【答案】
(1)證明:直線l的方程為(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.
化為:m(﹣x+2y+3)+(2x+y+4)=0,令 ![]() ,解得
,解得 ![]() ,
,
則直線l經過定點Q(﹣1,﹣2)
(2)解:當m變化時,PQ⊥直線l時,
點P(3,1)到直線l的距離的最大= ![]() =5
=5
(3)解:由于直線l經過定點Q(﹣1,﹣2).直線l的斜率k存在且k≠0,
因此可設直線l的方程為y+2=k(x+1),
可得與x軸、y軸的負半軸交于A( ![]() ,0),B(0,k﹣2)兩點,
,0),B(0,k﹣2)兩點,
![]() <0,k﹣2<0,解得k<0.
<0,k﹣2<0,解得k<0.
∴∴S△OAB= ![]() ×
× ![]() ×(2﹣k)=
×(2﹣k)= ![]() ≥2+
≥2+ ![]() =4,當且僅當k=﹣2時取等號.
=4,當且僅當k=﹣2時取等號.
此時直線l的方程為:y+2=﹣2(x+1),化為:2x+y+4=0
【解析】(1)直線l的方程為(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.化為:m(﹣x+2y+3)+(2x+y+4)=0,令 ![]() ,解出即可得出直線l經過定點.(2)當m變化時,PQ⊥直線l時,點P(3,1)到直線l的距離的最大.(3)由于直線l經過定點Q(﹣1,﹣2).直線l的斜率k存在且k≠0,因此可設直線l的方程為y+2=k(x+1),可得與x軸、y軸的負半軸交于A(
,解出即可得出直線l經過定點.(2)當m變化時,PQ⊥直線l時,點P(3,1)到直線l的距離的最大.(3)由于直線l經過定點Q(﹣1,﹣2).直線l的斜率k存在且k≠0,因此可設直線l的方程為y+2=k(x+1),可得與x軸、y軸的負半軸交于A( ![]() ,0),B(0,k﹣2)兩點,
,0),B(0,k﹣2)兩點, ![]() <0,k﹣2<0,解得k<0.可得S△OAB=
<0,k﹣2<0,解得k<0.可得S△OAB= ![]() ×
× ![]() ×(2﹣k)=
×(2﹣k)= ![]() ,利用基本不等式的性質即可得出.
,利用基本不等式的性質即可得出.


科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),
=(cosβ,sinβ), ![]() =({1,0).
=({1,0).
(1)求向量 ![]() +
+ ![]() 的長度的最大值;
的長度的最大值;
(2)設α= ![]() ,
, ![]() <β<
<β< ![]() ,且
,且 ![]() ⊥(
⊥( ![]() ﹣
﹣ ![]() ),求
),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的圖象如圖所示,下列數值排序正確的是( ) 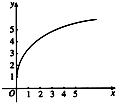
A.0<f′(2)<f′(3)<f(3)﹣f(2)
B.0<f′(3)<f(3)﹣f(2)<f′(2)
C.0<f(3)<f′(2)<f(3)﹣f(2)
D.0<f(3)﹣f(2)<f′(2)<f′(3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C1: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,且過點(1,
,且過點(1, ![]() ).
).
(1)求C1的方程;
(2)設直線l同時與橢圓C1和拋物線C2:y2=4x相切,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的離心率
的離心率 ![]() ,過點A(0,﹣b)和B(a,0)的直線與原點的距離為
,過點A(0,﹣b)和B(a,0)的直線與原點的距離為 ![]() .
.
(1)求橢圓的方程;
(2)已知定點E(﹣1,0),若直線y=kx+2(k≠0)與橢圓交于C、D兩點,問:是否存在k的值,使以CD為直徑的圓過E點?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于命題:若O是線段AB上一點,則有| ![]() |
| ![]() +|
+| ![]() |
| ![]() =
= ![]() .將它類比到平面的情形是:若O是△ABC內一點,則有S△OBC
.將它類比到平面的情形是:若O是△ABC內一點,則有S△OBC ![]() +S△OCA
+S△OCA ![]() +S△OBA
+S△OBA ![]() =
= ![]() ,將它類比到空間情形應該是:若O是四面體ABCD內一點,則有 .
,將它類比到空間情形應該是:若O是四面體ABCD內一點,則有 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線的頂點在原點,焦點在x軸,且拋物線上點P(2,m)到焦點的距離為3,斜率為2的直線L與拋物線相交于A,B兩點且|AB|=3 ![]() ,求拋物線和直線L的方程.
,求拋物線和直線L的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com