
【題目】已知![]() 是偶函數.
是偶函數.
(1)求![]() 的值;
的值;
(2)證明:對任意實數![]() ,函數
,函數![]() 的圖象與直線
的圖象與直線![]() 最多只有一個交點;
最多只有一個交點;
(3)設![]() 若函數
若函數![]() 的圖象有且只有一個公共點,求實數
的圖象有且只有一個公共點,求實數![]() 的取值范圍.
的取值范圍.
 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】冠狀病毒是一個大型病毒家族,己知可引起感冒以及中東呼吸綜合征(![]() )和嚴重急性呼吸綜合征(
)和嚴重急性呼吸綜合征(![]() )等較嚴重疾病.而今年出現在湖北武漢的新型冠狀病毒(
)等較嚴重疾病.而今年出現在湖北武漢的新型冠狀病毒(![]() )是以前從未在人體中發現的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發熱、咳嗽、氣促和呼吸困難等.在較嚴重病例中,感染可導致肺炎、嚴重急性呼吸綜合征、腎衰竭,甚至死亡.
)是以前從未在人體中發現的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發熱、咳嗽、氣促和呼吸困難等.在較嚴重病例中,感染可導致肺炎、嚴重急性呼吸綜合征、腎衰竭,甚至死亡.
某醫院為篩查冠狀病毒,需要檢驗血液是否為陽性,現有n(![]() )份血液樣本,有以下兩種檢驗方式:
)份血液樣本,有以下兩種檢驗方式:
方式一:逐份檢驗,則需要檢驗n次.
方式二:混合檢驗,將其中k(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗.
)份血液樣本分別取樣混合在一起檢驗.
若檢驗結果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數總共為![]() .
.
假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為p(![]() ).現取其中k(
).現取其中k(![]() 且
且![]() )份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為
)份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數為
,采用混合檢驗方式,樣本需要檢驗的總次數為![]() .
.
(1)若![]() ,試求p關于k的函數關系式
,試求p關于k的函數關系式![]() ;
;
(2)若p與干擾素計量![]() 相關,其中
相關,其中![]() (
(![]() )是不同的正實數,
)是不同的正實數,
滿足![]() 且
且![]() (
(![]() )都有
)都有![]() 成立.
成立.
(i)求證:數列![]() 等比數列;
等比數列;
(ii)當![]() 時,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數的期望值更少,求k的最大值
時,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數的期望值更少,求k的最大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的十九大報告明確指出要堅決打贏脫貧攻堅戰,讓貧困人口和貧困地區同全國一道進入全面小康社會,要動員全黨全國全社會力量,堅持精準扶貧、精準脫貧,確保到2020年我國現行標準下農村貧困人口實現脫貧.現有扶貧工作組到某山區貧困村實施脫貧工作.經摸底排查,該村現有貧困農戶100戶,他們均從事水果種植,2017年底該村平均每戶年純收入為1萬元,扶貧工作組一方面請有關專家對水果進行品種改良,提高產量;另一方面,抽出部分農戶從事水果包裝、銷售工作,其戶數必須小于種植的戶數.從2018年初開始,若該村抽出![]() 戶(
戶(![]() ,
,![]() )從事水果包裝、銷售.經測算,剩下從事水果種植農戶的年純收入每戶平均比上一年提高
)從事水果包裝、銷售.經測算,剩下從事水果種植農戶的年純收入每戶平均比上一年提高![]() ,而從事包裝銷售農戶的年純收入每戶平均為
,而從事包裝銷售農戶的年純收入每戶平均為![]() 萬元.(參考數據:
萬元.(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
(1)至2018年底,該村每戶年均純收入能否達到1.32萬元?若能,請求出從事包裝、銷售的戶數;若不能,請說明理由;
(2)至2020年底,為使從事水果種植農戶能實現脫貧(即每戶(水果種植農戶)年均純收入不低于1.6萬元),至少要抽出多少戶從事包裝、銷售工作?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司收取快遞費用的標準是:重量不超過![]() 的包裹收費10元;重量超過
的包裹收費10元;重量超過![]() 的包裹,除收費10元之外,超過
的包裹,除收費10元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
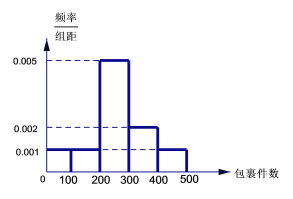
(1)求這60天每天包裹數量的平均值和中位數;
(2)該公司從收取的每件快遞的費用中抽取5元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.已知公司前臺有工作人員3人,每人每天工資100元,以樣本估計總體,試估計該公司每天的利潤有多少元?
(3)小明打算將![]() 四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過
四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過![]() ,求他支付的快遞費為45元的概率.
,求他支付的快遞費為45元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() 為自然對數的底數. 設
為自然對數的底數. 設![]() 是
是![]() 的導函數.
的導函數.
(Ⅰ)若![]() 時,函數
時,函數![]() 在
在![]() 處的切線經過點
處的切線經過點![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函數![]() 在區間
在區間![]() 上的單調區間;
上的單調區間;
(Ⅲ)若![]() ,函數
,函數![]() 在區間
在區間![]() 內有零點,求
內有零點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() .若
.若![]() 為線段
為線段![]() 的中點,則在
的中點,則在![]() 翻折過程中,有下列三個命題:
翻折過程中,有下列三個命題:
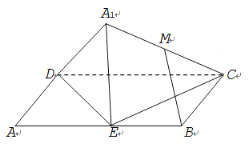
①線段![]() 的長是定值;
的長是定值;
②存在某個位置,使![]() ;
;
③存在某個位置,使![]() 平面
平面![]() .
.
其中正確的命題有______. (填寫所有正確命題的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】斐波那契數列0,1,1,2,3,5,8,13,…,是意大利數學家列昂納多·斐波那契發明的,定義如下:![]() ,
,![]() ,
,![]() .某同學設計了一個求解斐波那契數列前
.某同學設計了一個求解斐波那契數列前![]() 項和的程序框圖,如圖所示,若輸出
項和的程序框圖,如圖所示,若輸出![]() 的值為232,則處理框和判斷框中應該分別填入( )
的值為232,則處理框和判斷框中應該分別填入( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com