
已知數列{an}滿足條件: a1=1,a2=r(r>0),且{anan+1}是公比為q(q>0)的等比數列,設bn=a2n-1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2>an+2an+3(n∈N*)成立的q的取值范圍;
(2)求bn和![]() ,其中Sn=b1+b2+…+bn;
,其中Sn=b1+b2+…+bn;
(3)設r=219.2-1,q=![]() ,求數列{
,求數列{![]() }的最大項和最小項的值.
}的最大項和最小項的值.
(1) 0<q<![]() ; (2)
; (2)  (3) {Cn}的最大項C21=2.25,最小項C20=-4
(3) {Cn}的最大項C21=2.25,最小項C20=-4
(1)由題意得rqn-1+rqn>rqn+1.
由題設r>0,q>0,故從上式可得![]() q2-q-1<0,解得
q2-q-1<0,解得![]() <q<
<q<![]() ,因q>0,故0<q<
,因q>0,故0<q<![]() ;
;
(2)∵![]() .
.
b1=1+r≠0,所以{bn}是首項為1+r,公比為q的等比數列,從而bn=(1+r)qn-1.
當q=1時,Sn=n(1+r), ![]()
![]()
![]()
![]()
![]()
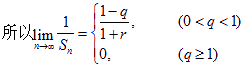
![]()
![]()
![]() ,從上式可知,
,從上式可知,
當n-20.2>0,即n≥21(n∈N*)時,Cn隨n的增大而減小,
故1<Cn≤C21=1+![]() =2.25 ①
=2.25 ①
當n-20.2<0,即n≤20(n∈N*)時,Cn也隨n的增大而減小,
故1>Cn≥C20=1+![]() =-4 ②
=-4 ②
綜合①②兩式知,對任意的自然數n有C20≤Cn≤C21,
故{Cn}的最大項C21=2.25,最小項C20=-4。


科目:高中數學 來源: 題型:
| 3+4an |
| 12-4an |
| 1 | ||
an-
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com