
撫州一中2009屆高三第四次模擬考試
數(shù)學(xué)試卷(文)
命題人 :高三數(shù)學(xué)組 考試時(shí)間 :2009.5
第Ⅰ卷(選擇題 共60分)
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
1.設(shè)集合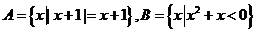 ,則
,則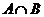 等于 ( )
等于 ( )

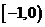

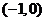

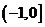

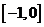
2.若曲線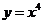 的一條切線
的一條切線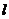 的斜率為
的斜率為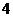 ,則切線
,則切線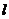 的方程是 ( )
的方程是 ( )



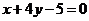

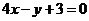

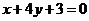
3.已知三條不重合的直線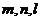 ,兩個(gè)不重合的平面
,兩個(gè)不重合的平面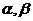 ,有下列命題
,有下列命題
①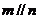 ,
,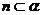
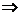
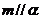 ; ②
; ②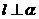 ,
,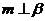 ,
,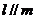
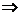
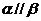 ;
;
③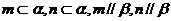
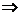
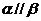 ;
;
④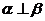 ,
,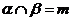 ,
,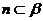 ,
,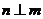
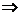
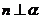 .
.
其中正確的命題個(gè)數(shù)是 ( )

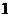



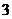

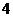
4.從圓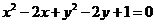 外一點(diǎn)
外一點(diǎn)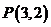 向這個(gè)圓作兩條切線,則兩切線夾角的余弦值為( )
向這個(gè)圓作兩條切線,則兩切線夾角的余弦值為( )



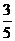

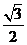
5.若關(guān)于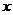 的不等式
的不等式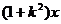
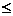
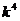 +4的解集是
+4的解集是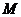 ,則對(duì)任意實(shí)常數(shù)
,則對(duì)任意實(shí)常數(shù)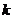 ,總有( )
,總有( )

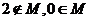

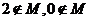

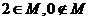

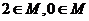
6.已知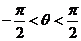 ,且
,且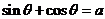 ,其中
,其中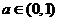 ,則
,則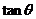 的值有可能是( )
的值有可能是( )

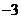

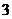 或
或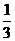

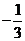 或
或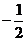

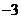 或
或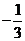
7.設(shè) 為
為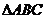 所在平面內(nèi)一點(diǎn),且
所在平面內(nèi)一點(diǎn),且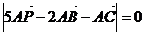 ,則
,則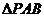 的面積與
的面積與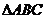 的面積之比為 ( )
的面積之比為 ( )

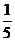

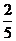

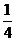

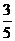
8.二項(xiàng)式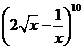 展開(kāi)式中,所有有理項(xiàng)(不含
展開(kāi)式中,所有有理項(xiàng)(不含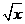 的項(xiàng))的系數(shù)之和為 ( )
的項(xiàng))的系數(shù)之和為 ( )

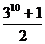

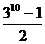

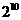

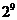
9.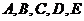 五人爭(zhēng)奪某項(xiàng)比賽的前三名,組織者對(duì)前三名發(fā)給不同的獎(jiǎng)品,若
五人爭(zhēng)奪某項(xiàng)比賽的前三名,組織者對(duì)前三名發(fā)給不同的獎(jiǎng)品,若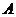 獲獎(jiǎng),
獲獎(jiǎng),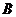 不是第一名,則不同的發(fā)獎(jiǎng)方式共有 ( )
不是第一名,則不同的發(fā)獎(jiǎng)方式共有 ( )
 72種
72種  30種
30種  24種
24種  14種
14種
10.?dāng)?shù)列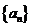 滿足:
滿足: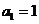 ,
,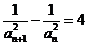 ,
,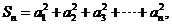 若
若
對(duì)于任意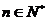 都成立,則正整數(shù)
都成立,則正整數(shù)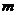 的最小值為( )www.wwwtb789.com
的最小值為( )www.wwwtb789.com

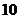

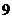

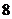

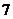
11.在直角坐標(biāo)系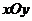 中,過(guò)雙曲線
中,過(guò)雙曲線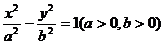 的左焦點(diǎn)
的左焦點(diǎn)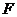 作圓
作圓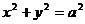 的一條切線(切點(diǎn)為
的一條切線(切點(diǎn)為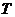 )交雙曲線右支于點(diǎn)
)交雙曲線右支于點(diǎn) ,若
,若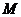 為
為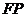 的中點(diǎn)。則
的中點(diǎn)。則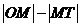 等于( )
等于( )

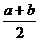

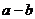

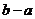

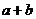
12.若實(shí)數(shù)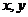 滿足
滿足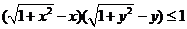 ,則 ( )
,則 ( )

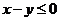

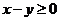

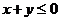

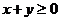
第Ⅱ卷(非選擇題 共90分)
二、填空題:本大題共4小題,每小題4分,共16分.把答案填在題中橫線上.
13.將函數(shù)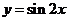 按向量
按向量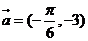 平移后得到的函數(shù)表達(dá)式是
;
平移后得到的函數(shù)表達(dá)式是
;
14.已知點(diǎn)A,B,C,D在同一球面上,AB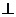 平面
平面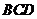 ,
,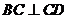 ,若
,若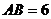 ,
,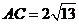 ,
,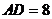 ,則B、C兩點(diǎn)間的球面距離是 ;
,則B、C兩點(diǎn)間的球面距離是 ;
15.如果點(diǎn)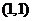 在不等式組
在不等式組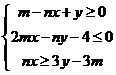 所表示的平面區(qū)域內(nèi),則
所表示的平面區(qū)域內(nèi),則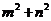 的取值范圍是 ;
的取值范圍是 ;
16.已知函數(shù) 與
與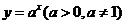 的圖象關(guān)于直線
的圖象關(guān)于直線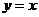 對(duì)稱,
對(duì)稱,
設(shè)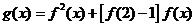 ,若
,若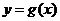 在區(qū)間
在區(qū)間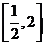 上是增函數(shù),則實(shí)數(shù)
上是增函數(shù),則實(shí)數(shù)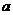 的取值范圍是 .
的取值范圍是 .
三、解答題:本大題共6小題,共74分.解答應(yīng)寫出文字說(shuō)明,證明過(guò)程或演算步驟.
17.(本題滿分12分)
已知四棱錐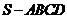 的底面
的底面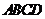 是正方形,側(cè)棱
是正方形,側(cè)棱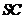 的中點(diǎn)
的中點(diǎn)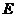 在底面內(nèi)的射影恰好是正方形
在底面內(nèi)的射影恰好是正方形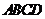 的中心
的中心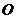 ,頂點(diǎn)
,頂點(diǎn)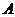 在截面
在截面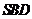 內(nèi)的射影恰好是
內(nèi)的射影恰好是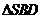 的重心
的重心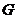 .
.
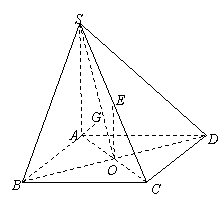 (1)求直線
(1)求直線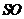 與底面
與底面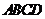 所成角的正切值;
所成角的正切值;
(2)設(shè)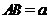 ,求此四棱錐過(guò)點(diǎn)
,求此四棱錐過(guò)點(diǎn)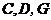 的截面面積.
的截面面積.
18.(本題滿分12分)
某工廠由于工作失誤,未貼標(biāo)簽前,把3箱含“三聚氰胺”的問(wèn)題牛奶與合格的3箱牛
奶混到了一起。對(duì)這6箱牛奶逐箱進(jìn)行檢測(cè),到確定出3箱問(wèn)題奶粉為止。
(1)求通過(guò)3次檢測(cè),就可以把3箱含“三聚氰胺”的牛奶全部篩選出來(lái)的概率;
(2)求最多通過(guò)4次檢測(cè),就可以把3箱含“三聚氰胺”的牛奶全部篩選很出來(lái)的概率。
19.(本題滿分12分)
在銳角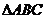 中,已知
中,已知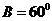 ,且
,且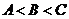 ,
,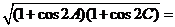
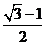 .
.
(1)求角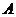 與
與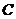 的大小;
的大小;
(2)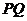 是以
是以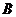 為圓心,
為圓心,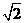 為半徑的圓的直徑,已知
為半徑的圓的直徑,已知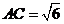 ,求
,求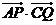 的最大值.
的最大值.
20.(本題滿分12分)
已知函數(shù)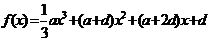 ,
,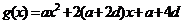 ,其中
,其中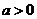 ,
,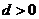 ,設(shè)
,設(shè)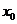 為
為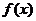 的極小值點(diǎn),
的極小值點(diǎn),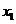 為
為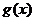 的極值點(diǎn),
的極值點(diǎn),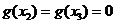 ,并且
,并且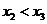 ,將點(diǎn)
,將點(diǎn)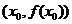 ,
,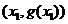 ,
,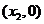 ,
,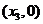 依次記為
依次記為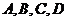 .
.
(1)求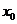 的值;
的值;
(2)若四邊形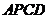 為梯形且面積為
為梯形且面積為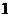 ,求
,求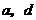 的值.
的值.
21.(本題滿分12分)
已知橢圓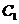 的方程為
的方程為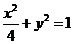 ,雙曲線
,雙曲線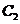 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為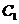 的左、右頂點(diǎn),而
的左、右頂點(diǎn),而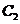 的左、右頂點(diǎn)分別是
的左、右頂點(diǎn)分別是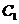 的左、右焦點(diǎn).
的左、右焦點(diǎn).
(1)求雙曲線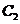 的方程;
的方程;
(2)若直線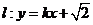 與橢圓
與橢圓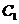 及雙曲線
及雙曲線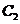 都恒有兩個(gè)不同的交點(diǎn),且
都恒有兩個(gè)不同的交點(diǎn),且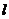 與
與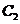 的兩個(gè)交點(diǎn)A和B滿足
的兩個(gè)交點(diǎn)A和B滿足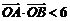 (其中
(其中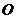 為原點(diǎn)),求k的取值范圍.
為原點(diǎn)),求k的取值范圍.
22.(本題滿分14分)
數(shù)列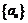 的通項(xiàng)是關(guān)于
的通項(xiàng)是關(guān)于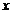 的不等式
的不等式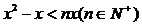 的解集中整數(shù)的個(gè)數(shù),
的解集中整數(shù)的個(gè)數(shù),
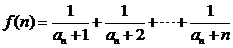 .
.
(1)求數(shù)列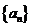 的通項(xiàng)公式;
的通項(xiàng)公式;
(2) 若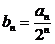 ,求
,求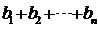 的和
的和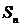 ;
;
(3) 求證:對(duì)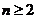 且
且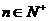 恒有
恒有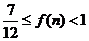 .
.
撫州一中2009屆高三第四次模擬考試
一、選擇題
題號(hào)
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
D
C
A
A
B
A
C
D
二、填空題13. ; 14.
; 14. ; 15.
; 15. ; 16.
; 16. .
.
三、解答題
17.(1)


 兩兩相互垂直, 連結(jié)
兩兩相互垂直, 連結(jié) 并延長(zhǎng)交
并延長(zhǎng)交 于F.
于F.


同理可得



 ------------ (6分)
------------ (6分)
(2) 是
是 的重心, F是SB的中點(diǎn)
的重心, F是SB的中點(diǎn)


梯形的高
 --- (12分)
--- (12分)
【注】可以用空間向量的方法
18.解:
(1)設(shè)通過(guò)3次檢測(cè),就可以把3箱含“三聚氰胺”的牛奶全部篩選出來(lái)的事件為A
 1分
1分
P(A)=
 5分
5分
所以通過(guò)3次檢測(cè),就可以把3箱含“三聚氰胺”的牛奶全部篩選出來(lái)的概率為
 …6分
…6分
(2)設(shè)最多通過(guò)4次檢測(cè),就可以把3箱含“三聚氰胺”的牛奶全部篩選出來(lái)的事件為B … 7分
P(B)=
 11分
11分
所以最多通過(guò)4次檢測(cè),就可以把3箱含“三聚氰胺”的牛奶全部篩選出來(lái)的概率為
 … 12分
… 12分
19.(1) .
.
又
 .
.

 .………6分
.………6分
(2)


又 ,
,
 .從而
.從而

當(dāng) 且同向時(shí),
且同向時(shí), .………12分
.………12分
20.解:(1)  ,
,
令 ,由
,由 得
得 或
或 .
. .
.
 .
.
當(dāng) 時(shí),
時(shí), ,當(dāng)
,當(dāng) 時(shí),
時(shí), ,所以
,所以 處取極小值,即
處取極小值,即 …………4分
…………4分
(2)

 處取得極小值,即
處取得極小值,即 由
由 即
即





由四邊形ABCD是梯形及BC與AD不平行,得 .有
.有 即
即
由四邊形ABCD的面積為1,得 即
即 得
得 ,從而
,從而 得
得 ……12分
……12分
21.(1)設(shè)雙曲線C2的方程為 = 1,則a2 = 4 ? 1 = 3,再由a2 + b2
= c2得b2 = 1.故C2的方程為
= 1,則a2 = 4 ? 1 = 3,再由a2 + b2
= c2得b2 = 1.故C2的方程為 = 1. (5分)
= 1. (5分)
(2)將y = kx + 代入
代入 得(1 + 4k2)x2 + 8
得(1 + 4k2)x2 + 8 kx + 4 = 0,由直線l與橢圓C1恒有兩個(gè)不同的交點(diǎn)得
kx + 4 = 0,由直線l與橢圓C1恒有兩個(gè)不同的交點(diǎn)得 (8
(8 )2k2 ? 16 (1 +
4k2) = 16(4k2 ? 1)>0,即k2>
)2k2 ? 16 (1 +
4k2) = 16(4k2 ? 1)>0,即k2> .①(7分)
.①(7分)
將y = kx +  代入
代入 得(1 ? 3k2)x2 ? 6
得(1 ? 3k2)x2 ? 6 kx ? 9 = 0.由直線l與雙曲線C2恒有兩個(gè)不同的交點(diǎn)A、B得
kx ? 9 = 0.由直線l與雙曲線C2恒有兩個(gè)不同的交點(diǎn)A、B得 .即k≠
.即k≠ 且k2<1.②(9分)
且k2<1.②(9分)
設(shè)A (xA,yA),B (xB,yB),則xA + xB
=  ,xA,xB =
,xA,xB =  ,由
,由 得xA xB +
yA yB<6,而xA xB +
yA yB = xA xB + (kxA +
得xA xB +
yA yB<6,而xA xB +
yA yB = xA xB + (kxA +  ) (kxb +
) (kxb +  )= (k2 + 1) xA xB +
)= (k2 + 1) xA xB +  k (xA + xB) + 2 = (k2 + 1)?
k (xA + xB) + 2 = (k2 + 1)? ,于是
,于是 <6,即將
<6,即將 .解此不等式得
.解此不等式得 或
或 .
③ (11分)
.
③ (11分)
由①、②、③得 ,
,
故k的取值范圍為
 . (12分)
. (12分)
22.(1) .
.
(2)
 ,
,
則 ,
,
 .
.
(3)
 ,
,
即 ①
①
又由于 ,
,
則 ,
,
兩式相減得 ,
,
 ,
, 當(dāng)
當(dāng) 且
且 時(shí)是增函數(shù),
時(shí)是增函數(shù),
 的最小值是
的最小值是 , ②
, ②
由①②得:  成立.
成立.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com