
2008年山東省淄博市中等學校招生考試
數學試卷
第Ⅰ卷(選擇題 共36分)
一、選擇題:本題共12小題,在每小題所給出的四個選項中,只有一個是正確的,請把正確的選項涂在答題卡的相應位置上。每小題3分,錯選、不選、選出的答案超過一個,均記0分。
1. 的相反數是
的相反數是
A.  B.
B. 
 C. 3 D. -3
C. 3 D. -3
2.下列運算正確的是
A. B.
B. C.
C. D.
D. 
3.如圖, ,要使a∥b,則∠2等于
,要使a∥b,則∠2等于

A.75° B.95° C.105° D.115°
4.與 是同類二次根式的是
是同類二次根式的是
A. B.
B. C.
C. D.-
D.-
5.如圖,在RT△ABC中,tanB=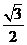 ,BC=
,BC= ,則AC等于
,則AC等于
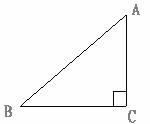
A. 3 B. 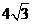 D.6
D.6
6.下面是四位同學對他們學習小組將要共同進行的一次統計活動分別設計的活動程序,其中正確的是
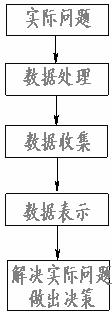
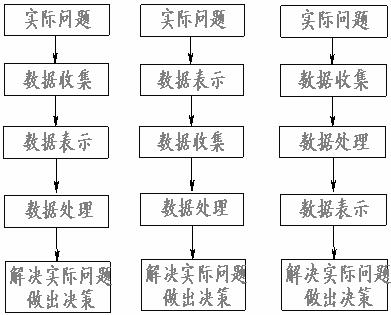
A. B. C. D.
7.已知點(-2,y1),(-1,y2),(3,y3),和(-3,-2)都在反比例函數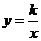 的圖象上,那么y1,y2 ,與y3的大小關系是
的圖象上,那么y1,y2 ,與y3的大小關系是
A.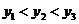
 B.
B.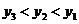 C.
C.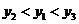 D.
D.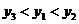
8.如圖,由4個小正方形組成的田字格中,△ABC的頂點都是小正方形的頂點。在田字格上畫與△ABC成軸對稱的三角形,且頂點都是小正方形的頂點,則這樣的三角形(不包含△ABC本身)共有
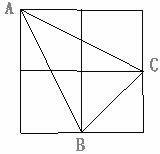
A.1個 B.2個 C.3個 D.4個
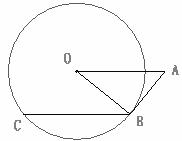
9.如圖,A是半徑為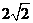 的⊙O外一點,OA=4,AB是⊙O的切線,點B是切點,弦
的⊙O外一點,OA=4,AB是⊙O的切線,點B是切點,弦
BC∥OA,則BC的長為
A. 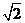
 B.
B. 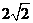 D.4
D.4
10.小紅設計了一個計算程序,并按此程序進行了兩次計算。在計算中輸入了不同的x值,
但一次沒有結果,另一次輸出的結果是42,則這兩次輸入的x值不可能是
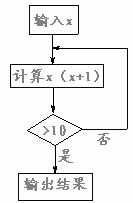
A. 0,2 B. -1,-
11.如圖,已知△ABC三個頂點的坐標分別為(1,2),(-2,3),(-1,0),把它們的橫坐標和縱坐標分別變成原來的2倍,得到點A′,B′,C′。下列說法正確的是
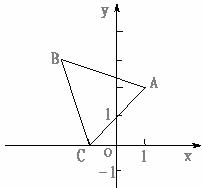
A.△A′B′C′與△ABC是位似圖形,位似中心是點(1,0)
B.△A′B′C′與△ABC是位似圖形,位似中心是點(0,0)
C.△A′B′C′與△ABC是相似圖形,但不是位似圖形
D.△A′B′C′與△ABC不是相似圖形
12.觀察下面幾組數:
1,3,5,7,9,11,13,15,……
2,5,8,11,14,17,20,23,……
7,13,19,25,31,37,43,49,……
這三組數具有共同的特點。
現在有上述特點的一組數,第一個數是3,第三個數是11,則其第n個數為
A.8-5 B.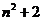
 C. 4n-1 D.
C. 4n-1 D.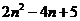
第Ⅱ卷 (菲選擇題 共84分)
二、填空題:本題共5小題,滿分20分。只要求填寫最后結果,每小題填對得4分。
13.若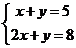 則x+2y=_________________.
則x+2y=_________________.
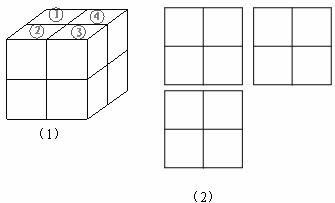
14.如圖(1),用八個同樣大小的小立方體搭成一個大立方體,小明從上面的四個小立方體中取走了兩個后,得到的新幾何體的三視圖如圖(2)所示,則他拿走的兩個小立方體的序號是_________________________.(只填寫滿足條件的一種情況即可)
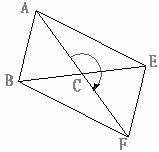
15.如圖,在△ABC中,AB=AC,將△ABC繞點C旋轉180°得到△FEC,連接AE,BF。當∠ACB為________________度時,四邊形ABFE為矩形。
16.在-9,-6,-3,-1,2,3,6,8,11這九個數中,任取一個作為a值,能夠使關
于x的一元二次方程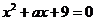 有兩個不相等的實數根的概率是_______________.
有兩個不相等的實數根的概率是_______________.
17.關于x的不等式組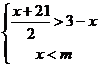 的所有整數解的和是-7,則m的取值范圍是___
的所有整數解的和是-7,則m的取值范圍是___
________________________________.
三、解答題:本大題共8小題,共64分。解答要寫出必要的文字說明、證明過程或演算步驟。
18.(本題滿分6分)
計算: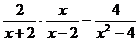
19.(本體滿分6分)
已知:如圖,AD與BC相交于點O,∠CAB=∠DBA,AC=BD,求證:
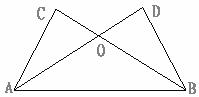
(1)∠C=∠D;
(2)△AOC≌△BOD.
20.(本題滿分8分)
2007年底,某校初四年級一班的同學曾經到學校附近的農貿市場調查了這個市場里100家商戶中的10家。這10家商戶平均每天送出的超薄塑料購物袋數量分別為(單位:把):
4 5 3 8 5 7 5 6 3 4
(1)請分別寫出這組數據的眾數、中位數;
(2)如果要選擇一種統計圖來表示這10家商戶送出的超薄塑料購物袋的情況,在條形統計圖、折線統計圖、扇形統計圖中你會選擇哪一個?
(3)已知一把超薄塑料購物袋有50個。通過對樣本的計算,估計該農貿市場一年要送出多少個超薄塑料購物袋(一年按350個營業日計算)?結果用科學記數法表示。
21.(本題滿分8分)
把長為
22.(本題滿分8分)
如圖,AB是⊙O的直徑,∠BAC的平分線AQ交BC于點P,交⊙O于點Q.已知AC=6,∠AQC=30°
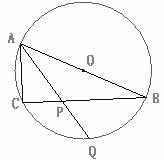
(1)求AB的長;
(2)求點P到AB的距離;
(3)求PQ的長。
23.(本題滿分8分)
甲、乙兩個倉庫要向A、B兩地調運小麥,已知甲庫可以調出80噸,乙庫可以調出40噸。A地需要小麥50噸,B地需要小麥70噸。甲、乙兩庫運往A、B地的費用如下表:
A地(元/噸)
B地(元/噸)
甲庫
10
40
乙庫
20
30
(1)設甲庫運往A地x噸,求總運費y(單位:元)與x之間的函數關系式;
(2)那種方案總運費最省?哪種方案總運費最多?并求最省和最多的運費。
24.(本題滿分10分)
一條拋物線經過點O與A(4,0)點,頂點B在直線y=kx+2k(k≠0)上。將這條拋物線先向上平移m(m>0)個單位,再向右平移m個單位,得到的拋物線的頂點仍然落在直線y=kx+2k上,點A移動到了點A′.
(1) 求K值及拋物線的表達式;
(2) 求使△A′OB′的面積是6032的m值。
25.(本題滿分10分)
正方形ABCD的對角線交點為O,兩條對角線把它分成了四個面積相等的三角形。
(1)平行四邊形ABCD的兩條對角線交點為O,若△AOB,△BOC,△COD,△DOA面積分別為S1,S2,S3,S4,試判斷S1,S2,S3,S4的關系,并加以證明;
(2)四邊形ABCD的兩條對角線互相垂直,交點為O,若△AOB,△BOC,△COD,△DOA面積分別為S1,S2,S3,S4,試判斷S1,S2,S3,S4的關系,并加以證明;
(3)四邊形ABCD的兩條對角線交點為O,若△AOB,△BOC,△COD,△DOA面積分別為S1,S2,S3,S4,試判斷S1,S2,S3,S4的關系,并加以證明;
(4)四邊形ABCD的兩條對角線相等,交點為O,∠BAC=∠BDC,若△AOB,△BOC,△COD,△DOA面積分別為S1,S2,S3,S4,試只用S1,S3或只用S2,S4表示四邊形ABCD的面積S.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com