
2008年黃石市初中畢業(yè)生學業(yè)考試
數(shù)學試卷
(閉卷 考試時間:120分鐘 滿分120分)
一、單項選擇題(本大題共12個小題,每小題3分,滿分36分)
1.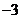 的相反數(shù)是( )
的相反數(shù)是( )
A. B.
B.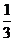 C.
C. D.
D.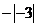
2.在實數(shù) ,
, ,
, ,
, ,
,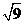 中,無理數(shù)有( )
中,無理數(shù)有( )
A.1個 B.2個 C.3個 D.4個
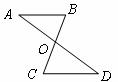
3.如圖, ,
, 和
和 相交于點
相交于點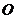 ,
, ,
,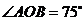 ,則
,則 等于( )
等于( )
A. B.
B. C.
C.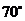 D.
D.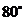
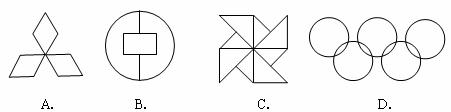
4.下列圖形中既是軸對稱圖形,又是中心對稱圖形的是( )
5.若不等式組 有實數(shù)解,則實數(shù)
有實數(shù)解,則實數(shù) 的取值范圍是( )
的取值范圍是( )
A.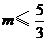 B.
B. C.
C. D.
D.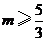
6.在反比例函數(shù)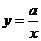 中,當
中,當 時,
時, 隨
隨 的增大而減小,則二次函數(shù)
的增大而減小,則二次函數(shù)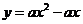 的圖象大致是下圖中的(
)
的圖象大致是下圖中的(
)
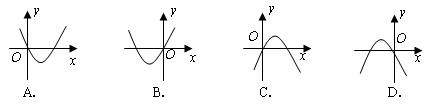
7.下面左圖所示的幾何體的俯視圖是( )
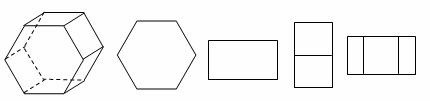
A B C D
8.如圖,每個小正方形邊長均為1,則下列圖中的三角形(陰影部分)與左圖中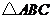 相似的是( )
相似的是( )

9.若一組數(shù)據(jù)2,4, ,6,8的平均數(shù)是6,則這組數(shù)據(jù)的方差是(
)
,6,8的平均數(shù)是6,則這組數(shù)據(jù)的方差是(
)
A.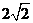 B.
B. D.40
D.40
10.若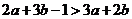 ,則
,則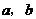 的大小關(guān)系為( )
的大小關(guān)系為( )
A. B.
B.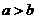 C.
C. D.不能確定
D.不能確定
11.已知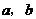 是關(guān)于
是關(guān)于 的一元二次方程
的一元二次方程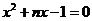 的兩實數(shù)根,則式子
的兩實數(shù)根,則式子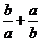 的值是( )
的值是( )
A.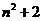 B.
B. C.
C.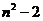 D.
D.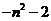
12.如圖,在等腰三角形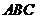 中,
中, ,點
,點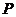 是底邊
是底邊 上一個動點,
上一個動點,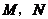 分別是
分別是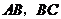 的中點,若
的中點,若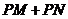 的最小值為2,則
的最小值為2,則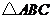 的周長是( )
的周長是( )

A.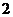 B.
B.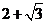 C.
C.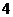 D.
D.
二、填空題(本大題共6個小題,每小題3分,滿分18分)
13.分解因式: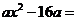 .
.
14.已知 是
是 的一次函數(shù),下表列出了部分對應值,則
的一次函數(shù),下表列出了部分對應值,則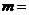 .
.

1
0
2

3

5
15.如圖,在 中,
中,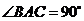 ,
,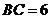 ,點
,點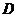 為
為 中點,將
中點,將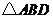 繞點
繞點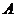 按逆時針方向旋轉(zhuǎn)
按逆時針方向旋轉(zhuǎn) 得到
得到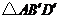 ,則點
,則點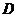 在旋轉(zhuǎn)過程中所經(jīng)過的路程為
.(結(jié)果保留
在旋轉(zhuǎn)過程中所經(jīng)過的路程為
.(結(jié)果保留 )
)

16.如圖,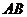 為⊙
為⊙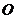 的直徑,點
的直徑,點 在⊙
在⊙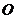 上,
上,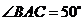 ,則
,則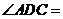 .
.

17.下圖是根據(jù)某初中為地震災區(qū)捐款的情況而制作的統(tǒng)計圖,已知該校在校學生有2000人,請根據(jù)統(tǒng)計圖計算該校共捐款 元.

18.若實數(shù)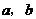 滿足
滿足 ,則
,則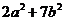 的最小值是 .
的最小值是 .
三、解答題(本大題共9個小題,滿分66分)
19.(本小題滿分6分)
計算
20.(本小題滿分6分)
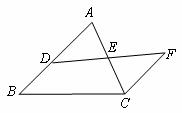
如圖,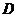 是
是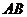 上一點,
上一點,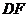 交
交 于點
于點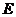 ,
, ,
, .
.
求證: .
.
21.(本小題滿分6分)先化簡后求值.
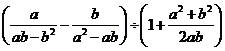 ,其中
,其中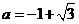 ,
,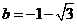 .
.
22.(本小題滿分7分)
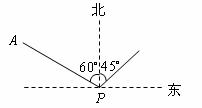
如圖,甲船在港口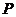 的北偏西
的北偏西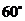 方向,距港口
方向,距港口 海里的
海里的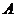 處,沿
處,沿 方向以12海里/時的速度駛向港口
方向以12海里/時的速度駛向港口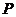 .乙船從港口
.乙船從港口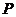 出發(fā),沿北偏東
出發(fā),沿北偏東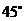 方向勻速駛離港口
方向勻速駛離港口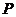 ,現(xiàn)兩船同時出發(fā),2小時后乙船在甲船的正東方向.求乙船的航行速度.(精確到0.1海里/時,參考數(shù)據(jù)
,現(xiàn)兩船同時出發(fā),2小時后乙船在甲船的正東方向.求乙船的航行速度.(精確到0.1海里/時,參考數(shù)據(jù) ,
,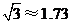 )
)
23.(本小題滿分7分)
某車間要生產(chǎn)220件產(chǎn)品,做完100件后改進了操作方法,每天多加工10件,最后總共用4天完成了任務.求改進操作方法后,每天生產(chǎn)多少件產(chǎn)品?
24.(本小題滿分7分)
在一個口袋中有 個小球,其中兩個是白球,其余為紅球,這些球的形狀、大小、質(zhì)地等完全相同,在看不到球的條件下,從袋中隨機地取出一個球,它是紅球的概率是
個小球,其中兩個是白球,其余為紅球,這些球的形狀、大小、質(zhì)地等完全相同,在看不到球的條件下,從袋中隨機地取出一個球,它是紅球的概率是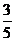 .
.
(1)求 的值;
的值;
(2)把這 個球中的兩個標號為1,其余分別標號為2,3,…,
個球中的兩個標號為1,其余分別標號為2,3,…,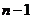 ,隨機地取出一個小球后不放回,再隨機地取出一個小球,求第二次取出小球標號大于第一次取出小球標號的概率.
,隨機地取出一個小球后不放回,再隨機地取出一個小球,求第二次取出小球標號大于第一次取出小球標號的概率.
25.(本小題滿分8分)
某公司有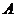 型產(chǎn)品40件,
型產(chǎn)品40件,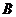 型產(chǎn)品60件,分配給下屬甲、乙兩個商店銷售,其中70件給甲店,30件給乙店,且都能賣完.兩商店銷售這兩種產(chǎn)品每件的利潤(元)如下表:
型產(chǎn)品60件,分配給下屬甲、乙兩個商店銷售,其中70件給甲店,30件給乙店,且都能賣完.兩商店銷售這兩種產(chǎn)品每件的利潤(元)如下表:
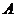 型利潤
型利潤
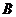 型利潤
型利潤
甲店
200
170
乙店
160
150
(1)設(shè)分配給甲店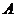 型產(chǎn)品
型產(chǎn)品 件,這家公司賣出這100件產(chǎn)品的總利潤為
件,這家公司賣出這100件產(chǎn)品的總利潤為 (元),求
(元),求 關(guān)于
關(guān)于 的函數(shù)關(guān)系式,并求出
的函數(shù)關(guān)系式,并求出 的取值范圍;
的取值范圍;
(2)若公司要求總利潤不低于17560元,說明有多少種不同分配方案,并將各種方案設(shè)計出來;
(3)為了促銷,公司決定僅對甲店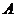 型產(chǎn)品讓利銷售,每件讓利
型產(chǎn)品讓利銷售,每件讓利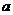 元,但讓利后
元,但讓利后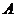 型產(chǎn)品的每件利潤仍高于甲店
型產(chǎn)品的每件利潤仍高于甲店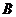 型產(chǎn)品的每件利潤.甲店的
型產(chǎn)品的每件利潤.甲店的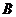 型產(chǎn)品以及乙店的
型產(chǎn)品以及乙店的 型產(chǎn)品的每件利潤不變,問該公司又如何設(shè)計分配方案,使總利潤達到最大?
型產(chǎn)品的每件利潤不變,問該公司又如何設(shè)計分配方案,使總利潤達到最大?
26.(本小題滿分9分)
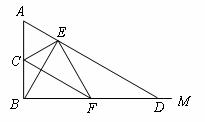
如圖, 為直角,點
為直角,點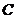 為線段
為線段 的中點,點
的中點,點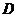 是射線
是射線 上的一個動點(不與點
上的一個動點(不與點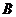 重合),連結(jié)
重合),連結(jié) ,作
,作 ,垂足為
,垂足為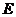 ,連結(jié)
,連結(jié) ,過點
,過點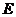 作
作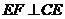 ,交
,交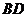 于
于 .
.
(1)求證: ;
;
(2)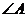 在什么范圍內(nèi)變化時,四邊形
在什么范圍內(nèi)變化時,四邊形 是梯形,并說明理由;
是梯形,并說明理由;
(3)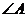 在什么范圍內(nèi)變化時,線段
在什么范圍內(nèi)變化時,線段 上存在點
上存在點 ,滿足條件
,滿足條件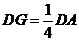 ,并說明理由.
,并說明理由.
27.(本小題滿分10分)
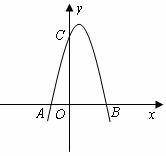
如圖,已知拋物線與 軸交于點
軸交于點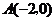 ,
,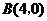 ,與
,與 軸交于點
軸交于點 .
.
(1)求拋物線的解析式及其頂點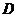 的坐標;
的坐標;
(2)設(shè)直線 交
交 軸于點
軸于點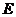 .在線段
.在線段 的垂直平分線上是否存在點
的垂直平分線上是否存在點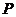 ,使得點
,使得點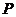 到直線
到直線 的距離等于點
的距離等于點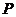 到原點
到原點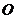 的距離?如果存在,求出點
的距離?如果存在,求出點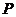 的坐標;如果不存在,請說明理由;
的坐標;如果不存在,請說明理由;
(3)過點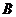 作
作 軸的垂線,交直線
軸的垂線,交直線 于點
于點 ,將拋物線沿其對稱軸平移,使拋物線與線段
,將拋物線沿其對稱軸平移,使拋物線與線段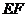 總有公共點.試探究:拋物線向上最多可平移多少個單位長度?向下最多可平移多少個單位長度?
總有公共點.試探究:拋物線向上最多可平移多少個單位長度?向下最多可平移多少個單位長度?
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com