
題目列表(包括答案和解析)
在 中,
中,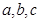 ,分別是角
,分別是角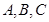 所對邊的長,
所對邊的長,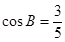 ,且
,且
(1)求 的面積;
的面積;
(2)若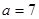 ,求角C.
,求角C.
【解析】第一問中,由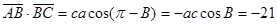 又∵
又∵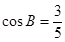 ∴
∴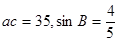 ∴
∴ 的面積為
的面積為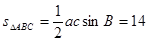
第二問中,∵a =7 ∴c=5由余弦定理得: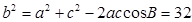 得到b的值,然后又由余弦定理得:
得到b的值,然后又由余弦定理得: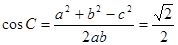
又C為內角 ∴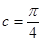
解:(1)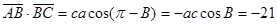 ………………2分
………………2分
又∵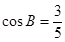 ∴
∴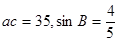 ……………………4分
……………………4分
∴ 的面積為
的面積為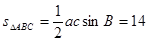 ……………………6分
……………………6分
(2)∵a =7 ∴c=5 ……………………7分
由余弦定理得: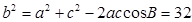
∴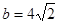 ……………………9分
……………………9分
又由余弦定理得: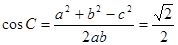
又C為內角 ∴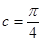 ……………………12分
……………………12分
另解:由正弦定理得: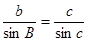 ∴
∴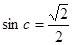 又
又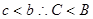 ∴
∴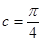
已知在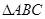 中,
中,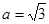 ,
,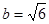 ,
,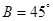 ,解這個三角形;
,解這個三角形;
【解析】本試題主要考查了正弦定理的運用。由正弦定理得到: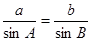
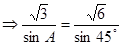 ,然后又
,然后又 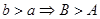
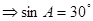
又 再又
再又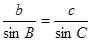 得到c。
得到c。
解:由正弦定理得到: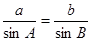
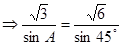
又 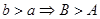
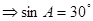 ……4分
……4分
又 ……8分
……8分
又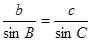
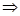
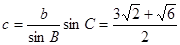
給出問題:已知 滿足
滿足 ,試判定
,試判定 的形狀.某學生的解答如下:
的形狀.某學生的解答如下:
解:(i)由余弦定理可得,
 ,
,

 ,
,

 ,
,
故 是直角三角形.
是直角三角形.
(ii)設 外接圓半徑為
外接圓半徑為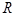 .由正弦定理可得,原式等價于
.由正弦定理可得,原式等價于

 ,
,
故 是等腰三角形.
是等腰三角形.
綜上可知, 是等腰直角三角形.
是等腰直角三角形.
請問:該學生的解答是否正確?若正確,請在下面橫線中寫出解題過程中主要用到的思想方法;若不正確,請在下面橫線中寫出你認為本題正確的結果. .
已知函數 .]
.]
(1)求函數 的最小值和最小正周期;
的最小值和最小正周期;
(2)設 的內角
的內角 、
、 、
、 的對邊分別為
的對邊分別為 ,
, ,
, ,且
,且 ,
, ,
,
若 ,求
,求 ,
, 的值.
的值.
【解析】第一問利用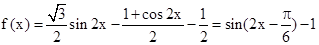
得打周期和最值
第二問

 ,由正弦定理,得
,由正弦定理,得 ,①
,①
由余弦定理,得 ,即
,即 ,②
,②
由①②解得
設△ABC的內角A、B、C所對的邊分別為a、b、c,已知a=1,b=2,cosC=. (1)求△ABC的周長; (2)求cos(A-C)的值.
【解析】(1)借助余弦定理求出邊c,直接求周長即可.(2)根據兩角差的余弦公式需要求sinC,sinA,cosA,由正弦定理即可求出sinA,進而可求出cosA.sinC可由cosA求出,問題得解.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com