
題目列表(包括答案和解析)
【2012高考江蘇26】(10分)設集合![]() ,
,![]() .記
.記![]() 為同時滿足下列條件的集合
為同時滿足下列條件的集合![]() 的個數:
的個數:
①![]() ;②若
;②若![]() ,則
,則![]() ;③若
;③若![]() ,則
,則![]() 。
。
(1)求![]() ;
;
(2)求![]() 的解析式(用
的解析式(用![]() 表示).
表示).
某市投資甲、乙兩個工廠,2011年兩工廠的產量均為100萬噸,在今后的若干年內,甲工廠的年產量每年比上一年增加10萬噸,乙工廠第 年比上一年增加
年比上一年增加 萬噸,記2011年為第一年,甲、乙兩工廠第
萬噸,記2011年為第一年,甲、乙兩工廠第 年的年產量分別為
年的年產量分別為 萬噸和
萬噸和 萬噸.
萬噸.
(Ⅰ)求數列 ,
, 的通項公式;
的通項公式;
(Ⅱ)若某工廠年產量超過另一工廠年產量的2倍,則將另一工廠兼并,問到哪一年底,其中哪一個工廠被另一個工廠兼并.
【解析】本試題主要考查數列的通項公式的運用。
第一問由題得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98
第二問,考查等差數列與等比數列的綜合,考查用數列解決實際問題,其步驟是建立數列模型,進行計算得出結果,再反饋到實際中去解決問題.由于比較兩個工廠的產量時兩個函數的形式較特殊,不易求解,故采取了列舉法,數據列舉時作表格比較簡捷.
解:(Ⅰ)由題得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98……6分
(Ⅱ)由于n,各年的產量如下表
n 1 2 3 4 5 6 7 8
an 100 110 120 130 140 150 160 170
bn 100 102 106 114 130 162 226 354
2015年底甲工廠將被乙工廠兼并
一個袋中裝有四個形狀大小完全相同的球,球的編號分別為1,2,3,4.
(I)從袋中隨機抽取一個球,將其編號記為 ,然后從袋中余下的三個球中再隨機抽取一個球,將其編號記為
,然后從袋中余下的三個球中再隨機抽取一個球,將其編號記為 .求關于
.求關于 的一元二次方程
的一元二次方程 有實根的概率;
有實根的概率;
(II)先從袋中隨機取一個球,該球的編號為m,將球放回袋中,然后再從袋中隨機取一個球,該球的編號為n.若以 作為點P的坐標,求點P落在區域
作為點P的坐標,求點P落在區域 內的概率.
內的概率.
【解析】第一問利用古典概型概率求解所有的基本事件數共12種,然后利用方程 有實根,則滿足△=4a2-4b2≥0,即a2≥b2。,這樣求得事件發生的基本事件數為6種,從而得到概率。第二問中,利用所有的基本事件數為16種。即基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4) (3,1)
(3,2) (3,3)
(3,4) (4,1) (4,2) (4,3)
(4,4)共16種。在求解滿足
有實根,則滿足△=4a2-4b2≥0,即a2≥b2。,這樣求得事件發生的基本事件數為6種,從而得到概率。第二問中,利用所有的基本事件數為16種。即基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4) (3,1)
(3,2) (3,3)
(3,4) (4,1) (4,2) (4,3)
(4,4)共16種。在求解滿足 的基本事件數為(1,1) (2,1) (2,2) (3,1) 共4種,結合古典概型求解得到概率。
的基本事件數為(1,1) (2,1) (2,2) (3,1) 共4種,結合古典概型求解得到概率。
(1)基本事件(a,b)有:(1,2) (1,3) (1,4) (2,1) (2,3) (2,4) (3,1) (3,2) (3,4) (4,1) (4,2) (4,3)共12種。
∵ 有實根, ∴△=4a2-4b2≥0,即a2≥b2。
有實根, ∴△=4a2-4b2≥0,即a2≥b2。
記“ 有實根”為事件A,則A包含的事件有:(2,1) (3,1)
(3,2) (4,1) (4,2) (4,3) 共6種。
有實根”為事件A,則A包含的事件有:(2,1) (3,1)
(3,2) (4,1) (4,2) (4,3) 共6種。
∴PA.=  。 …………………6分
。 …………………6分
(2)基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4) (2,1) (2,2) (2,3) (2,4) (3,1) (3,2) (3,3) (3,4) (4,1) (4,2) (4,3) (4,4)共16種。
記“點P落在區域 內”為事件B,則B包含的事件有:
內”為事件B,則B包含的事件有:
(1,1) (2,1) (2,2) (3,1) 共4種。∴PB.=
某省環保研究所對市中心每天環境放射性污染情況進行調查研究后,發現一天中環境綜合放射性污染指數 與時刻
與時刻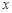 (時) 的關系為
(時) 的關系為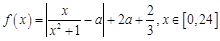 ,其中
,其中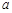 是與氣象有關的參數,且
是與氣象有關的參數,且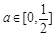 .
.
(1)令 ,
, 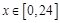 ,寫出該函數的單調區間,并選擇其中一種情形進行證明;
,寫出該函數的單調區間,并選擇其中一種情形進行證明;
(2)若用每天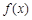 的最大值作為當天的綜合放射性污染指數,并記作
的最大值作為當天的綜合放射性污染指數,并記作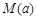 ,求
,求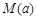 ;
;
(3)省政府規定,每天的綜合放射性污染指數不得超過2,試問目前市中心的綜合放射性污染指數是否超標?
【解析】第一問利用定義法求證單調性,并判定結論。
第二問(2)由函數的單調性知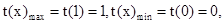 ,
,
∴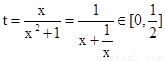 ,即t的取值范圍是
,即t的取值范圍是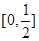 .
.
當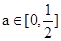 時,記
時,記
則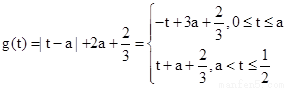
∵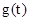 在
在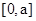 上單調遞減,在
上單調遞減,在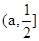 上單調遞增,
上單調遞增,
第三問因為當且僅當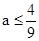 時,
時,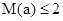 .
.
故當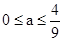 時不超標,當
時不超標,當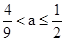 時超標.
時超標.
改革開放以來,我國高等教育事業有了突飛猛進的發展,有人記錄了某村 到
到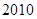 年十年間每年考入大學的人數.為方便計算,
年十年間每年考入大學的人數.為方便計算, 年編號為
年編號為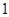 ,
,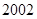 年編號為
年編號為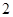 ,…,
,…,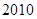 年編號為
年編號為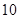 .數據如下:
.數據如下:
|
年份( |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
人數( |
3 |
5 |
8 |
11 |
13 |
14 |
17 |
22 |
30 |
31 |
(1)從這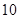 年中隨機抽取兩年,求考入大學的人數至少有
年中隨機抽取兩年,求考入大學的人數至少有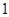 年多于
年多于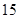 人的概率;
人的概率;
(2)根據前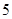 年的數據,利用最小二乘法求出
年的數據,利用最小二乘法求出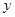 關于
關于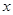 的回歸方程
的回歸方程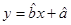 ,并計算第
,并計算第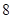 年的估計值和實際值之間的差的絕對值。
年的估計值和實際值之間的差的絕對值。
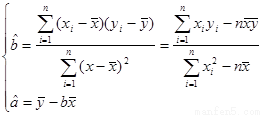
【解析】(1)設考入大學人數至少有1年多于15人的事件為A則P(A)=1-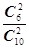 =
=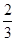 (4’)
(4’)
(2)由已知數據得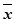 =3,
=3,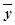 =8,
=8,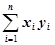 =3+10+24+44+65=146
=3+10+24+44+65=146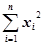 =1+4+9+16+25=55(7’)
=1+4+9+16+25=55(7’)
則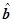 =
=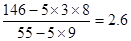 ,
,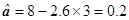 (9’)
(9’)
則回歸直線方程為y=2.6x+0.2 (10’)
則第8年的估計值和真實值之間的差的絕對值為
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com