精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

已知曲線的參數(shù)方程是（是參數(shù)），以坐標(biāo)原點為極點，軸的正半軸為極軸建立極坐標(biāo)系，曲線:的極坐標(biāo)方程是=2，正方形ABCD的頂點都在上，且A,B,C,D依逆時針次序排列，點A的極坐標(biāo)為（2，）.

(Ⅰ)求點A,B,C,D的直角坐標(biāo)；

 (Ⅱ)設(shè)P為上任意一點，求的取值范圍.

【命題意圖】本題考查了參數(shù)方程與極坐標(biāo)，是容易題型.

【解析】(Ⅰ)由已知可得，，

，，

即A(1，)，B（－，1），C（―1，―），D（，－1），

(Ⅱ)設(shè)，令=，

則==，

∵，∴的取值范圍是[32,52]

現(xiàn)有4個人去參加某娛樂活動，該活動有甲、乙兩個游戲可供參加者選擇.為增加趣味性，約定：每個人通過擲一枚質(zhì)地均勻的骰子決定自己去參加哪個游戲，擲出點數(shù)為1或2的人去參加甲游戲，擲出點數(shù)大于2的人去參加乙游戲.

（Ⅰ）求這4個人中恰有2人去參加甲游戲的概率；

（Ⅱ）求這4個人中去參加甲游戲的人數(shù)大于去參加乙游戲的人數(shù)的概率；

（Ⅲ）用X，Y分別表示這4個人中去參加甲、乙游戲的人數(shù)，記，求隨機(jī)變量的分布列與數(shù)學(xué)期望.

【解析】依題意，這4個人中，每個人去參加甲游戲的概率為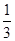，去參加乙游戲的概率為.

設(shè)“這4個人中恰有i人去參加甲游戲”為事件

則.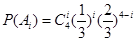

（1）這4個人中恰有2人去參加甲游戲的概率

（2）設(shè)“這4個人中去參加甲游戲的人數(shù)大于去參加乙游戲的人數(shù)”為事件B，則.由于互斥，故

所以，這個人中去參加甲游戲的人數(shù)大于去參加乙游戲的人數(shù)的概率為.

（3）的所有可能取值為0,2,4.由于互斥，互斥，故

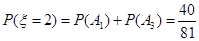
所以的分布列是

隨機(jī)變量的數(shù)學(xué)期望.

某校從參加高三年級理科綜合物理考試的學(xué)生中隨機(jī)抽出名學(xué)生，將其數(shù)學(xué)成績（均為整數(shù)）分成六段，…后得到如下部分頻率分布直方圖.觀察圖形的信息，回答下列問題：

（Ⅰ）求分?jǐn)?shù)在內(nèi)的頻率，并補(bǔ)全這個頻率分布直方圖；

（Ⅱ）統(tǒng)計方法中，同一組數(shù)據(jù)常用該組區(qū)間的中點值作為代表，據(jù)此估計本次考試的

平均分；

（Ⅲ）若從名學(xué)生中隨機(jī)抽取人，抽到的學(xué)生成績在記分，在記分，

在記分，用表示抽取結(jié)束后的總記分，求的分布列和數(shù)學(xué)期望.

【解析】（1）中利用直方圖中面積和為1，可以求解得到分?jǐn)?shù)在內(nèi)的頻率為

（2）中結(jié)合平均值可以得到平均分為：

（3）中用表示抽取結(jié)束后的總記分x, 學(xué)生成績在的有人，在的有人，在的有人,結(jié)合古典概型的概率公式求解得到。

(Ⅰ)設(shè)分?jǐn)?shù)在內(nèi)的頻率為，根據(jù)頻率分布直方圖，則有，可得，所以頻率分布直方圖如右圖.……4分

（求解頻率3分，畫圖1分）

（Ⅱ）平均分為：……7分

（Ⅲ）學(xué)生成績在的有人，在的有人，

在的有人.并且的可能取值是.    ………8分

則；； ；

；.（每個1分）

所以的分布列為

…………………13分

已知數(shù)列的通項公式，

，試通過計算的值，推測出的值。

【解析】本試題主要考查了數(shù)列通項公式的運用和歸納猜想思想的運用。由的通項公式得到，，并根據(jù)結(jié)果可猜想。

解：……………………2分

    …………4分

    …………6分

由此猜想，

如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

（Ⅰ）證明PC⊥AD；

（Ⅱ）求二面角A-PC-D的正弦值；

（Ⅲ）設(shè)E為棱PA上的點，滿足異面直線BE與CD所成的角為30°，求AE的長.

【解析】解法一：如圖，以點A為原點建立空間直角坐標(biāo)系，依題意得A(0,0,0)，D(2,0,0),C(0,1,0), 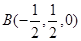,P（0,0,2）.

（1）證明：易得，于是,所以

(2) ,設(shè)平面PCD的法向量，

則,即.不防設(shè)，可得.可取平面PAC的法向量于是從而.

所以二面角A-PC-D的正弦值為.

（3）設(shè)點E的坐標(biāo)為（0,0，h），其中，由此得.

由，故 

所以，，解得，即.

解法二：（1）證明：由，可得，又由,,故.又,所以.

(2)如圖，作于點H，連接DH.由,,可得.

因此,從而為二面角A-PC-D的平面角.在中，,由此得由（1）知,故在中，

因此所以二面角的正弦值為.

（3）如圖，因為，故過點B作CD的平行線必與線段AD相交，設(shè)交點為F，連接BE，EF. 故或其補(bǔ)角為異面直線BE與CD所成的角.由于BF∥CD，故.在中，故

在中，由,,

可得.由余弦定理，,

所以.