題目列表(包括答案和解析)
已知函數
（Ⅰ）試判斷函數
的單調性，并說明理由；（Ⅱ）若
恒成立，求實數
的取值范圍；（Ⅲ）求證： 
.
已知函數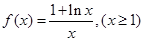
．
（Ⅰ）試判斷函數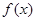
的單調性，并說明理由；
（Ⅱ）若
恒成立，求實數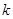
的取值范圍．
已知函數
．
（Ⅰ）試判斷函數
的單調性，并說明理由；
（Ⅱ）若
恒成立，求實數
的取值范圍．
已知函數
．
（1）試判斷函數
的單調性，并說明理由；
（2）若
恒成立，求實數
的取值范圍．
已知函數
．
（1）試判斷函數
的單調性，并說明理由；
（2）若
恒成立，求實數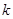
的取值范圍．
一．選擇題：
二、填空題: 13. 
14. 15. 
16. 
三．解答題
17．解：⑴f(x)= sinxcosx+
+cos2x =
sin(2x+
)+
T=π，2 kπ-
≤2x+≤2 kπ+，k∈Z,
最小正周期為π，單調增區間[kπ-
,kπ+
],k∈Z.
⑵由sin(2A+)=0,<2A+<
,
∴2A+=π或2π，∴A=或
18. 解：（1）
（2）設各等獎的獎金數為ξ則
ξ
5000
1000
20
0
P
0.001
0.009
0.09
0.9
∴Eξ=5+9+1.8+0=15.8（元）
19．解：（1）
平面
∵二面角
為直二面角，且
，
平面
平面
．
（2）連接
與高
交于
，連接
是邊長為2的正方形， 
，
二平面
，由三垂線定理逆定理得
是二面角
的平面角
由（1）
平面
，
．
在
中，
∴在
中，
故二面角等于
．
（2）可用向量法
20. 解：（1）因
故
是公比為
的等比數列，且
故
．
（2）由
得
注意到
，可得
，即
記數列
的前
項和為
，則
兩式相減得：
故
從而
．
21．解:（1）由
得
∴橢圓
的方程為：
．
（2）設直線
的方程為：
由
得
由此得
． ①
設與橢圓的交點為
，則
由
得
，整理得
，整理得
時，上式不成立，
②
由式①、②得
或
∴
取值范圍是
．
22.,解（1）
故
在
遞減
（2）
記
再令 
在上遞增
，從而 
故
在上也單調遞增
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com