
題目列表(包括答案和解析)
(本小題滿分13分)
對于定義域分別為![]() 的函數
的函數![]() ,規定:
,規定:
函數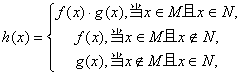
若函數![]() ,求函數
,求函數![]() 的取值集合;
的取值集合;
若![]() ,設
,設![]() 為曲線
為曲線![]() 在點
在點![]() 處切線的斜率;而
處切線的斜率;而![]() 是等差數列,公差為1
是等差數列,公差為1![]() ,點
,點![]() 為直線
為直線![]() 與
與![]() 軸的交點,點
軸的交點,點![]() 的坐標為
的坐標為![]() 。求證:
。求證:![]() ;
;
若![]() ,其中
,其中![]() 是常數,且
是常數,且![]() ,請問,是否存在一個定義域為
,請問,是否存在一個定義域為![]() 的函數
的函數![]() 及一個
及一個![]() 的值,使得
的值,使得![]() ,若存在請寫出一個
,若存在請寫出一個![]() 的解析式及一個
的解析式及一個![]() 的值,若不存在請說明理由。
的值,若不存在請說明理由。
(本題滿分15分)設M是由滿足下列條件的函數![]() 構成的集合:“①方程
構成的集合:“①方程![]() 有實數根;②函數
有實數根;②函數![]() 的導數
的導數![]() 滿足
滿足![]() ”
”
(I)證明:函數![]() 是集合M中的元素;
是集合M中的元素;
(II)證明:函數![]() 具有下面的性質:對于任意
具有下面的性質:對于任意![]()
![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。
成立。
(III)若集合M中的元素![]() 具有下面的性質:若
具有下面的性質:若![]() 的定義域為D,則對于任意[m,n]
的定義域為D,則對于任意[m,n]![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。試用這一性質證明:對集合M中的任一元素
成立。試用這一性質證明:對集合M中的任一元素![]() ,方程
,方程![]() 只有一個實數根。
只有一個實數根。
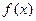 構成的集合:“①方程
構成的集合:“①方程 有實數根;②函數
有實數根;②函數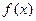 的導數
的導數 滿足
滿足 ”
” 是集合M中的元素;
是集合M中的元素; 具有下面的性質:對于任意
具有下面的性質:對于任意
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。 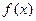 具有下面的性質:若
具有下面的性質:若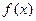 的定義域為D,則對于任意[m,n]
的定義域為D,則對于任意[m,n] ,都存在
,都存在 ,使得等式
,使得等式 成立。試用這一性質證明:對集合M中的任一元素
成立。試用這一性質證明:對集合M中的任一元素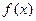 ,方程
,方程 只有一個實數根。
只有一個實數根。
| |||||||||||||||
一、填空題:
1.試題.files/image250.gif) 2.
2.試題.files/image252.gif) 3.
3.試題.files/image254.gif) 4.
4.試題.files/image256.gif) 5.
5.試題.files/image258.gif) 6.
6.試題.files/image260.gif) 7.
7.試題.files/image262.gif) 8.2009 9.4個 10.①② 11.
8.2009 9.4個 10.①② 11.試題.files/image264.gif)
二、選擇題:
12.B 13.C 14.D 15.D
三、解答題:
16.解:(Ⅰ)因為試題.files/image145.gif) 點的坐標為
點的坐標為試題.files/image154.gif) ,根據三角函數定義可知
,根據三角函數定義可知試題.files/image267.gif) ,
,
試題.files/image269.gif) ,
,試題.files/image271.gif) , 2分
, 2分
所以試題.files/image273.gif) 4分
4分
(Ⅱ)因為三角形試題.files/image156.gif) 為正三角形,所以
為正三角形,所以試題.files/image275.gif) ,
,試題.files/image277.gif) ,
,試題.files/image279.gif) ,
5分
,
5分
所以試題.files/image281.gif)
試題.files/image283.gif) 7分
7分
所以試題.files/image285.gif)
試題.files/image287.gif) 。
11分
。
11分
17.方法一:(I)證明:連結OC,因為試題.files/image289.gif) 所以
所以試題.files/image291.gif)
又試題.files/image293.gif) 所以
所以試題.files/image295.gif) ,
2分
,
2分
在試題.files/image297.gif) 中,由已知可得
中,由已知可得試題.files/image299.gif) 而
而試題.files/image301.gif)
所以試題.files/image303.gif) 所以
所以試題.files/image305.gif) 即
即試題.files/image307.gif) ,
,
而試題.files/image309.gif) 所以
所以試題.files/image175.gif) 平面
平面試題.files/image312.gif) 。
5分
。
5分
(II)解:取AC的中點M,連結OM、ME、OE,由E為BC的中點知試題.files/image314.gif)
所以直線OE與EM所成的銳角就是異面直線AB與CD所成的角, 7分
在試題.files/image316.gif) 中,
中,試題.files/image318.gif) 因為
因為試題.files/image320.gif) 是直角
是直角試題.files/image297.gif) 斜邊AC上的中線,所以
斜邊AC上的中線,所以試題.files/image323.gif) 所以
所以試題.files/image325.gif)
所以異面直線AB與CD所成角的大小為試題.files/image327.gif) 。
12分
。
12分
18.解:(Ⅰ)由年銷售量為試題.files/image187.gif) 件,按利潤的計算公式,有生產A、B兩產品的年利潤
件,按利潤的計算公式,有生產A、B兩產品的年利潤試題.files/image330.gif) 分別為:
分別為:
試題.files/image332.gif) 且
且試題.files/image334.gif) 2分
2分
試題.files/image336.gif)
所以試題.files/image338.gif) 5分
5分
(Ⅱ)因為試題.files/image340.gif) 所以
所以試題.files/image342.gif) 為增函數,
為增函數,
試題.files/image344.gif) ,所以
,所以試題.files/image346.gif) 時,生產A產品有最大利潤為
時,生產A產品有最大利潤為試題.files/image348.gif) (萬美元)
(萬美元)
又試題.files/image350.gif) ,所以
,所以試題.files/image352.gif) 時,生產B產品
時,生產B產品
有最大利潤為460(萬美元) 8分
現在我們研究生產哪種產品年利潤最大,為此,我們作差比較:
試題.files/image354.gif) 10分
10分
所以:當試題.files/image356.gif) 時,投資生產A產品200件可獲得最大年利潤;
時,投資生產A產品200件可獲得最大年利潤;
當試題.files/image358.gif) 時,生產A產品與生產B產品均可獲得最大年利潤;
時,生產A產品與生產B產品均可獲得最大年利潤;
當試題.files/image360.gif) 時,投資生產B產品100件可獲得最大年利潤。12分
時,投資生產B產品100件可獲得最大年利潤。12分
19.解:(1)當試題.files/image362.gif) 時,
時,試題.files/image364.gif) ,
,試題.files/image366.gif) 成立,所以
成立,所以試題.files/image197.gif) 是偶函數;
是偶函數;
3分
當試題.files/image369.gif) 時,
時,試題.files/image371.gif) ,這時
,這時試題.files/image373.gif) 所以
所以試題.files/image197.gif) 是非奇非偶函數;
6分
是非奇非偶函數;
6分
(2)當試題.files/image199.gif) 時,
時,試題.files/image376.gif) 設
設試題.files/image378.gif) 且
且試題.files/image380.gif) ,則
,則
試題.files/image382.gif) 9分
9分
當試題.files/image378.gif) 時,因為
時,因為試題.files/image378.gif) 且
且試題.files/image380.gif) ,所以
,所以試題.files/image385.gif)
所以試題.files/image387.gif) ,
,
試題.files/image389.gif) ,所以
,所以試題.files/image197.gif) 是區間
是區間試題.files/image202.gif) 的單調遞減函數。 14分
的單調遞減函數。 14分
20.解:(Ⅰ)由拋物線試題.files/image218.gif) :
:試題.files/image394.gif) 知
知試題.files/image396.gif) ,設
,設試題.files/image398.gif) ,
,試題.files/image214.gif) 在
在試題.files/image218.gif) 上,且
上,且試題.files/image220.gif) ,所以
,所以試題.files/image403.gif) ,得
,得試題.files/image405.gif) ,代入
,代入試題.files/image394.gif) ,得
,得試題.files/image407.gif) ,
,
所以試題.files/image409.gif) 。
4分
。
4分
試題.files/image214.gif) 在
在試題.files/image216.gif) 上,由已知橢圓
上,由已知橢圓試題.files/image216.gif) 的半焦距
的半焦距試題.files/image414.gif) ,于是
,于是試題.files/image416.gif)
消去試題.files/image418.gif) 并整理得
并整理得 試題.files/image420.gif) , 解得
, 解得試題.files/image422.gif) (
(試題.files/image424.gif) 不合題意,舍去).
不合題意,舍去).
故橢圓試題.files/image216.gif) 的方程為
的方程為試題.files/image427.gif) 。
7分
。
7分
(另法:因為試題.files/image214.gif) 在
在試題.files/image216.gif) 上,
上,
所以試題.files/image429.gif) ,所以
,所以試題.files/image422.gif) ,以下略。)
,以下略。)
(Ⅱ)由試題.files/image432.gif) 得
得試題.files/image434.gif) ,所以點O到直線
,所以點O到直線試題.files/image436.gif) 的距離為
的距離為
試題.files/image438.gif) ,又
,又試題.files/image440.gif) ,
,
所以試題.files/image442.gif) ,
,
試題.files/image444.gif) 且
且試題.files/image446.gif) 。
10分
。
10分
下面視提出問題的質量而定:
如問題一:當試題.files/image227.gif) 面積為
面積為試題.files/image448.gif) 時,求直線
時,求直線試題.files/image436.gif) 的方程。(
的方程。(試題.files/image451.gif) ) 得2分
) 得2分
問題二:當試題.files/image227.gif) 面積取最大值時,求直線
面積取最大值時,求直線試題.files/image436.gif) 的方程。(
的方程。(試題.files/image453.gif) ) 得4分
) 得4分
21.解:(1)
試題.files/image240.gif)
2
3
35
100
試題.files/image242.gif)
97
94
3
1
4分
(2)試題.files/image455.gif) 由題意知數列
由題意知數列試題.files/image230.gif) 的前34項成首項為100,公差為-3的等差數列,從第35項開始,奇數項均為3,偶數項均為1,
6分
的前34項成首項為100,公差為-3的等差數列,從第35項開始,奇數項均為3,偶數項均為1,
6分
從而試題.files/image244.gif) =
=試題.files/image458.gif) 8分
8分
=試題.files/image460.gif) 10分
10分
(3)證明:①若試題.files/image462.gif) ,則題意成立,
12分
,則題意成立,
12分
②若試題.files/image464.gif) ,此時數列
,此時數列試題.files/image230.gif) 的前若干項滿足
的前若干項滿足試題.files/image466.gif) ,即
,即試題.files/image468.gif) ,
,
設試題.files/image470.gif) ,則當
,則當試題.files/image472.gif) 時,
時,試題.files/image474.gif) ,
,
從而此時命題成立; 14分
③若試題.files/image476.gif) ,由題意得
,由題意得試題.files/image478.gif) ,則由②的結論知此時命題也成立,
,則由②的結論知此時命題也成立,
綜上所述,原命題成立。 16分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com