精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

設(shè)橢圓 ：（）的一個頂點(diǎn)為，，分別是橢圓的左、右焦點(diǎn)，離心率 ，過橢圓右焦點(diǎn) 的直線  與橢圓 交于 ， 兩點(diǎn)．

（1）求橢圓的方程；

（2）是否存在直線 ，使得 ，若存在，求出直線  的方程；若不存在，說明理由；

【解析】本試題主要考查了橢圓的方程的求解，以及直線與橢圓的位置關(guān)系的運(yùn)用。（1）中橢圓的頂點(diǎn)為，即又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061917121082894691/SYS201206191714546570844292_ST.files/image015.png">，得到，然后求解得到橢圓方程（2）中，對直線分為兩種情況討論，當(dāng)直線斜率存在時，當(dāng)直線斜率不存在時，聯(lián)立方程組，結(jié)合得到結(jié)論。

解：（1）橢圓的頂點(diǎn)為，即

，解得， 橢圓的標(biāo)準(zhǔn)方程為 --------4分

（2）由題可知,直線與橢圓必相交.

①當(dāng)直線斜率不存在時，經(jīng)檢驗(yàn)不合題意．                    --------5分

②當(dāng)直線斜率存在時，設(shè)存在直線為，且，.

由得，       ----------7分

，，               

   = 

所以，                               ----------10分

故直線的方程為或 

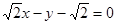即或

 

一條河的兩岸平行，河的寬度m，一艘船從處出發(fā)到河對岸．已知船的速度km/h，水流速度km/h．要使船行駛的時間最短，那么船行駛的距離與合速度的比值必須最小．此時我們分三種情況討論：

當(dāng)船逆流行駛，與水流成鈍角時；

當(dāng)船順流行駛，與水流成銳角時；

當(dāng)船垂直于對岸行駛，與水流成直角時．

請同學(xué)們計算上面三種情況，是否當(dāng)船垂直于對岸行駛時，與水流成直角時，所用時間最短

一條河的兩岸平行，河的寬度d=500 m，一艘船從A處出發(fā)到河對岸，已知船的速度|v₁|=10 km/h, 水流速度|v₂|=2 km/h,要使船行駛的時間最短，那么船行駛的距離與合速度的比值必須最小，分三種情況討論：

（1）當(dāng)船逆流行駛，與水流成鈍角時；

（2）當(dāng)船順流行駛，與水流成銳角時；

（3）當(dāng)船垂直于對岸行駛，與水流成直角時.

計算以上三種情況，是否當(dāng)船垂直于對岸行駛，與水流成直角時，所用時間最短.

一條河的兩岸平行，河的寬度m，一艘船從處出發(fā)到河對岸．已知船的速度km/h，水流速度km/h．要使船行駛的時間最短，那么船行駛的距離與合速度的比值必須最小．此時我們分三種情況討論：

當(dāng)船逆流行駛，與水流成鈍角時；

當(dāng)船順流行駛，與水流成銳角時；

當(dāng)船垂直于對岸行駛，與水流成直角時．

請同學(xué)們計算上面三種情況，是否當(dāng)船垂直于對岸行駛時，與水流成直角時，所用時間最短

已知函數(shù)，

（1）求函數(shù)的定義域；

（2）求函數(shù)在區(qū)間上的最小值；

（3）已知，命題p：關(guān)于x的不等式對函數(shù)的定義域上的任意恒成立；命題q：指數(shù)函數(shù)是增函數(shù)．若“p或q”為真，“p且q”為假，求實(shí)數(shù)m的取值范圍．

【解析】第一問中，利用由 即

第二問中，，得：

，

第三問中，由在函數(shù)的定義域上 的任意，，當(dāng)且僅當(dāng)時等號成立。當(dāng)命題p為真時，；而命題q為真時：指數(shù)函數(shù)．因?yàn)椤皃或q”為真，“p且q”為假，所以

當(dāng)命題p為真，命題q為假時；當(dāng)命題p為假，命題q為真時分為兩種情況討論即可 。

解：（1）由 即

（2），得：

，

（3）由在函數(shù)的定義域上 的任意，，當(dāng)且僅當(dāng)時等號成立。當(dāng)命題p為真時，；而命題q為真時：指數(shù)函數(shù)．因?yàn)椤皃或q”為真，“p且q”為假，所以

當(dāng)命題p為真，命題q為假時，

當(dāng)命題p為假，命題q為真時，，

所以