題目列表(包括答案和解析)
已知數列{an}的前n項和為Sn，點(n，
)在直線y＝
x＋
上；數列{bn}滿足bn+2－2bn+1－bn＝0(n∈N*)，且b3＝11，它的前9項和為153．
(1)求數列{an}、{bn}的通項公式；
(2)設cn＝
，數列{cn}的前n項和為Tn，求使不等式Tn＞
對一切n∈N*都成立的最大正整數k的值；
若實數x、y、m滿足|x－m|＞|y－m|，則稱x比y遠離m．
(1)若x2－1比1遠離0，求x的取值范圍；
(2)對任意兩個不相等的正數a、b，證明：a3＋b3比a2b＋ab2遠離2ab
；
(3)已知函數f(x)的定義域
．任取x∈D，f(x)等于sinx和cosx中遠離0的那個值.寫出函數f(x)的解析式，并指出它的基本性質(結論不要求證明)．
若實數x、y、m滿足|x－m|＜|y－m|，則稱x比y接近m．
(1)若x2－1比3接近0，求x的取值范圍；
(2)對任意兩個不相等的正數a、b，證明：a2b＋ab2比a3＋b3接近2ab
；
(3)已知函數f(x)的定義域D＝{x|x≠kπ，k∈Z，x∈R}．任取x∈D，f(x)等于1＋sinx和1－sinx中接近0的那個值．寫出函數f(x)的解析式，并指出它的奇偶性、最小正周期、最小值和單調性(結論不要求證明)．
已知函數f(t)對任意實數x、y都有：f(x＋y)＝f(x)＋f(y)＋3xy(x＋y＋2)＋3，且f(1)＝1．
(1)求f(0)、f(－1)、f(2)的值；
(2)若t為正整數，求f(t)的表達式．
(3)滿足條件f(t)＝t的所有整數t能否構成等差數列？若能構成等差數列，求出此數列；若不能構成等差數列，請說明理由．
已知二次函數f(x)＝ax2＋bx＋c的圖像的頂點坐標是(
，－
)，且f(3)＝2
(Ⅰ)求y＝f(x)的表達式，并求出f(1)，f(2)的值；
(Ⅱ)數列{an}，{bn}，若對任意的實數x都滿足g(x)·f(x)＋anx＋bn＝xn+1，n∈N*，其中g(x)是定義在實數R上的一個函數，求數列{an}、{bn}的通項公式；
(Ⅲ)設圓Cn：(x－an)2＋(y－bn)2＝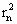
，若圓Cn與圓Cn+1外切，{rn}是各項都是正數的等比數列，記Sn是前n個圓的面積之和，求
．(n∈N*)
一、選擇題
1．D 2．A 3．C 4．D 5．B 6．C 7．D 8．B 9．A 10．A
二、填空題
11．148 12．－4 13．
14．－6 15．①②③④
三、解答題
16．解：⑴
＝
＝
＝
＝
3分
＝
＝1＋1＋2cos2x
＝2＋2cos2x
＝4cos2x
∵x∈[0，
] ∴cosx≥0
∴
＝2cosx 6分
⑵ f (x)＝cos2x－
?2cosx?sinx
＝cos2x－sin2x
＝2cos(2x＋
) 8分
∵0≤x≤ ∴
∴
∴
∴
，當x＝時取得該最小值
，當x＝0時取得該最大值 12分
17．由題意知，在甲盒中放一球概率為
，在乙盒放一球的概率為
3分
①當n＝3時，x＝3，y＝0的概率為
6分
②|x－y|＝2時，有x＝3，y＝1或x＝1，y＝3
它的概率為
12分
18．解：⑴證明：在正方形ABCD中，AB⊥BC
又∵PB⊥BC ∴BC⊥面PAB ∴BC⊥PA
同理CD⊥PA ∴PA⊥面ABCD 4分
⑵在AD上取一點O使AO=AD，連接E，O，
則EO∥PA，∴EO⊥面ABCD 過點O做
OH⊥AC交AC于H點，連接EH，則EH⊥AC，
從而∠EHO為二面角E－AC－D的平面角 6分
在△PAD中，EO＝AP＝
在△AHO中∠HAO＝45°，
∴HO＝AOsin45°=
，∴tan∠EHO＝
，
∴二面角E－AC－D等于arctan
8分
⑶當F為BC中點時，PF∥面EAC，理由如下：
∵AD∥2FC，∴
，又由已知有
，∴PF∥ES
∵PF
面EAC，EC
面EAC ∴PF∥面EAC，
即當F為BC中點時，PF∥面EAC 12分
19．⑴f '(x)＝3x2＋2bx＋c，由題知f '(1)＝0
3＋2b＋c＝0，
f (1)＝－11＋b＋c＋2＝－1
∴b＝1，c＝－5 3分
f (x)＝x3＋x2－5x＋2，f '(x)＝3x2＋2x－5
f (x)在[－
，1]為減函數，f (x)在(1，＋∞)為增函數
∴b＝1，c＝－5符合題意 5分
⑵即方程：
恰有三個不同的實解：
x3＋x2－5x＋2＝k(x≠0)
即當x≠0時，f (x)的圖象與直線y＝k恰有三個不同的交點，
由⑴知f (x)在
為增函數，
f (x)在
為減函數，f (x)在(1，＋∞)為增函數，
又
，f (1)＝－1，f (2)＝2
∴
且k≠2 12分
20．⑴∵
∴
3分
∴{an－3n}是以首項為a1－3＝2，公比為－2的等比數列
∴an－3n＝2?(－2)n－1
∴an＝3n＋2?(－2)n－1＝3n－(－2)n 6分
⑵由3nbn＝n?(3n－an)＝n?[3n－3n＋(－2)n]＝n?(－2)n
∴bn＝n?(－)n 8分
令
∴
∴
∴
＜6
∴m≥6 13分
21．⑴設M(x0，y0)，則N(x0，－y0)，P(x，y)
AM：y＝
①
BN：y＝
②
聯立①② ∴
4分
∵點M(xo，yo)在圓⊙O上，代入圓的方程：
整理：y2＝－2(x＋1) (x＜－1) 6分
⑵由
設S(x1、y1)，T(x2、y2)，ST的中點坐標(x0、y0)
則x1＋x2＝－(3＋
)
x1x2＝
8分
∴
中點到直線
的距離
∴
故圓與x＝－
總相切． 14分
⑵另解：∵y2＝－2(x＋1)知焦點坐標為(－
，0) 2分
頂點(－1，0)，故準線x＝－ 4分
設S、T到準線的距離為d1，d2，ST的中點O'，O'到x＝－的距離為
又由拋物線定義：d1＋d2＝|ST|，∴
故以ST為直徑的圓與x＝－總相切 8分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com